题目内容
10.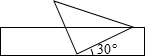 如图,将一个有45°角的三角板的直角顶点放在一张宽为4cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为( )
如图,将一个有45°角的三角板的直角顶点放在一张宽为4cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为( )| A. | 12cm | B. | 8cm | C. | 6$\sqrt{2}$cm | D. | 8$\sqrt{2}$cm |
分析 过另一个顶点C作垂线CD如图,可得直角三角形,根据直角三角形中30°角所对的边等于斜边的一半,可求出有45°角的三角板的直角边,再由等腰直角三角形求出最大边.
解答  解:过点C作CD⊥AD,∴CD=3,
解:过点C作CD⊥AD,∴CD=3,
在直角三角形ADC中,
∵∠CAD=30°,
∴AC=2CD=2×4=8,
又∵三角板是有45°角的三角板,
∴AB=AC=8,
∴BC2=AB2+AC2=82+82=128,
∴BC=8$\sqrt{2}$,
故选:D.
点评 本题考查了含30°角的直角三角形,及等腰直角三角形问题,关键是先由求得直角边,再由勾股定理求出最大边.

练习册系列答案
 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
18.在某中学开展的“书香伴我行”读书活动中,为了解九年级300名学生一个月的读书情况,随机调查了九年级50名学生读书的册数,统计数据如表所示:
估计这所中学九年级学生一个月共读书约648册,你的估计理由是50名学生读书的平均册数等于全年级学生读书的册数.
| 册数 | 0 | 1 | 2 | 3 | 4 |
| 人数 | 1 | 13 | 16 | 17 | 3 |
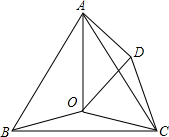 如图,点O是等边△ABC内一点,将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OA和OD.
如图,点O是等边△ABC内一点,将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OA和OD. 如图,在等腰梯形ABCD中,已知AD∥BC,AB=DC,AC与BD交于点O,延长BC到E,使得CE=AD,连接DE.
如图,在等腰梯形ABCD中,已知AD∥BC,AB=DC,AC与BD交于点O,延长BC到E,使得CE=AD,连接DE.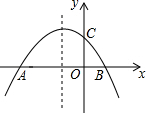 已知二次函数y=-x2-2x+3的图象与x轴分别交于A、B两点(如图所示),与y轴交于点C,点P是其对称轴上一动点,当PB+PC取得最小值时,点P的坐标为(-1,2).
已知二次函数y=-x2-2x+3的图象与x轴分别交于A、B两点(如图所示),与y轴交于点C,点P是其对称轴上一动点,当PB+PC取得最小值时,点P的坐标为(-1,2).