题目内容
2.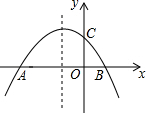 已知二次函数y=-x2-2x+3的图象与x轴分别交于A、B两点(如图所示),与y轴交于点C,点P是其对称轴上一动点,当PB+PC取得最小值时,点P的坐标为(-1,2).
已知二次函数y=-x2-2x+3的图象与x轴分别交于A、B两点(如图所示),与y轴交于点C,点P是其对称轴上一动点,当PB+PC取得最小值时,点P的坐标为(-1,2).
分析 首先求得A、B以及C的坐标,和函数对称轴的解析式,然后利用待定系数法求得AC的解析式,AC与二次函数的对称轴的交点就是P.
解答  解:连接AC.
解:连接AC.
在y=-x2-2x+3中,令y=0,则-x2-2x+3=0,
解得:x=-3或1.
则A的坐标是(-3,0),B的坐标是(1,0),
则对称轴是x=-1.
令x=0,解得y=3,则C的坐标是(0,3).
设经过A和C的直线的解析式是y=kx+b.
根据题意得:$\left\{\begin{array}{l}{-3k+b=0}\\{b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=3}\end{array}\right.$,
则AC的解析式是y=x+3,
令x=-1,则y=2.
则P的坐标是(-1,2 ).
故答案是(-1,2).
点评 本题考查了二次函数的坐标轴的交点,以及对称的性质,确定P的位置是本题的关键.

练习册系列答案
相关题目
10.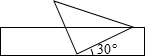 如图,将一个有45°角的三角板的直角顶点放在一张宽为4cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为( )
如图,将一个有45°角的三角板的直角顶点放在一张宽为4cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为( )
 如图,将一个有45°角的三角板的直角顶点放在一张宽为4cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为( )
如图,将一个有45°角的三角板的直角顶点放在一张宽为4cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为( )| A. | 12cm | B. | 8cm | C. | 6$\sqrt{2}$cm | D. | 8$\sqrt{2}$cm |
7.若x2=(-5)2,$\root{3}{{y}^{3}}$=-5,那么x+y的值是( )
| A. | 0 | B. | -10 | C. | 0或-10 | D. | 0或±10 |
 ?ABCD中,M、N为BD三等分点,则EN:EF=2:3.
?ABCD中,M、N为BD三等分点,则EN:EF=2:3. 如图,AB是⊙O的直径,AC、BC是⊙O的弦,若圆心O到AC的距离为1,且AC=2$\sqrt{3}$.
如图,AB是⊙O的直径,AC、BC是⊙O的弦,若圆心O到AC的距离为1,且AC=2$\sqrt{3}$.