题目内容
20．下列说法：①如果两个三角形可以用“ASA”来判定全等，那么也可以用“AAS”来判定它们全等；
②如果两个三角形都与第三个三角形全等，那么这两个三角形也全等；
③要判定两个三角形全等，给出的条件中至少要有一个三角形的一边与另一个三角形的一边相等．
其中正确的是（ ）
| A． | ①②③ | B． | ①和② | C． | ②和③ | D． | ①和③ |
分析 熟练运用判定定理判断，做题时要结合已知与全等的判定方法逐个验证．
解答 解：因为两个三角形的两个角对应相等，根据内角和定理，可知另一对对应角也相等，那么总能利用ASA来判定两个三角形全等，故选项①正确；
两个全等的直角三角形都和一个等边三角形不全等，但是这两个全等的直角三角形可以全等，故选项②错误；
判定两个三角形全等时，给出的条件中至少要有一个三角形的一边与另一个三角形的一边相等，故选项③正确．
故选A
点评 此题考查全等三角形的判定，AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．
练习册系列答案
相关题目
10．
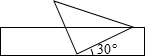如图，将一个有45°角的三角板的直角顶点放在一张宽为4cm的纸带边沿上．另一个顶点在纸带的另一边沿上，测得三角板的一边与纸带的一边所在的直线成30°角，如图，则三角板的最大边的长为（ ）
如图，将一个有45°角的三角板的直角顶点放在一张宽为4cm的纸带边沿上．另一个顶点在纸带的另一边沿上，测得三角板的一边与纸带的一边所在的直线成30°角，如图，则三角板的最大边的长为（ ）| A． | 12cm | B． | 8cm | C． | 6$\sqrt{2}$cm | D． | 8$\sqrt{2}$cm |
?ABCD中，M、N为BD三等分点，则EN：EF=2：3．
8．下面说法中正确的是（ ）
| A． | -2-1-3可以说是-2，-1，-3的和 | B． | -2-1-3可以说是2，-1，-3的和 | ||
| C． | -2-1-3是连减运算不能说成和 | D． | -2-1-3=-2+3-1 |
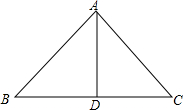如图，AB=AC，AD为△ABC的BC边上的中线，△ABD与△ACD全等吗？为什么？
如图，AB是⊙O的直径，AC、BC是⊙O的弦，若圆心O到AC的距离为1，且AC=2$\sqrt{3}$．
如图，在平面直角坐标系中，一段圆弧经过点A、B、C，其中点B的坐标为（4，3），则圆弧所在圆的半径为2$\sqrt{5}$．