题目内容
11.当k=±$\frac{2}{9}$时,一次函数y=kx+6的图象与坐标轴围成的三角形的面积是4.分析 先根据坐标轴上点的坐标特征求出一次函数与坐标的交点坐标(0,6),(-$\frac{6}{k}$,0),则根据三角形面积公式得到$\frac{1}{2}$•6•|-$\frac{6}{k}$|=4,然后解绝对值方程即可.
解答 解:当x=0时,y=kx+6=6,则一次函数与y轴的交点坐标为(0,6),
当y=0时,kx+6=0,解得x=-$\frac{6}{k}$,则一次函数与x轴的交点坐标为(-$\frac{6}{k}$,0),
所以$\frac{1}{2}$•6•|-$\frac{6}{k}$|=4,解得k=±$\frac{2}{9}$.
故答案为±$\frac{2}{9}$.
点评 本题考查了一次函数图象上点的坐标特征:直线上任意一点的坐标都满足函数关系式y=kx+b.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
10.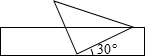 如图,将一个有45°角的三角板的直角顶点放在一张宽为4cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为( )
如图,将一个有45°角的三角板的直角顶点放在一张宽为4cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为( )
 如图,将一个有45°角的三角板的直角顶点放在一张宽为4cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为( )
如图,将一个有45°角的三角板的直角顶点放在一张宽为4cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为( )| A. | 12cm | B. | 8cm | C. | 6$\sqrt{2}$cm | D. | 8$\sqrt{2}$cm |
 如图,在直角坐标系中,直线AB交y轴正半轴于点A(0,4),交x轴正半轴于点B,在x轴负半轴上有一点C,连接AC,△AOC的面积为12,△AOB的面积为4.
如图,在直角坐标系中,直线AB交y轴正半轴于点A(0,4),交x轴正半轴于点B,在x轴负半轴上有一点C,连接AC,△AOC的面积为12,△AOB的面积为4.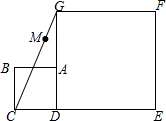 如图,四边形ABCD和四边形DEFG都是正方形.
如图,四边形ABCD和四边形DEFG都是正方形.