题目内容
16.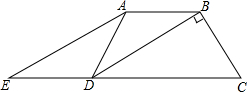 如图,在四边形ABCD中,AB=AD,BD平分∠ADC,E是CD的延长线上一点,且∠AEC=$\frac{1}{2}$∠ADC,求证:四边形ABDE是平行四边形.
如图,在四边形ABCD中,AB=AD,BD平分∠ADC,E是CD的延长线上一点,且∠AEC=$\frac{1}{2}$∠ADC,求证:四边形ABDE是平行四边形.
分析 由等腰三角形的性质得出∠ADB=∠ABD,由角平分线得出∠ADB=∠CDB,得出∠ABD=∠CDB,由内错角相等得出AB∥CE,再证出∠AEC=∠CDB,由同位角相等得出AE∥BD,即可得出结论.
解答 证明:∵AB=AD,
∴∠ADB=∠ABD,
∵BD平分∠ADC,
∴∠ADB=∠CDB,
∴∠ABD=∠CDB,
∴AB∥CE,
又∵∠AEC=$\frac{1}{2}$∠ADC,
∴∠AEC=∠CDB,
∴AE∥BD,
∴四边形ABDE是平行四边形.
点评 本题考查了平行四边形的判定、平行线的判定、等腰三角形的性质、角平分线的定义;熟练掌握等腰三角形的性质,弄清角之间的关系证出平行线是解决问题的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
1.地球是一颗行星,科学家测算得出银河系中大约有2000亿颗行星,地球以外尚未发现有生命的星球.2000亿用科学记数法表示为( )
| A. | 2×1011 | B. | 2×1012 | C. | 2×213 | D. | 2×1014 |
8.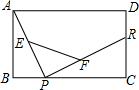 如图,已知长方形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动,而点R不动时,那么下列结论成立的是( )
如图,已知长方形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动,而点R不动时,那么下列结论成立的是( )
 如图,已知长方形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动,而点R不动时,那么下列结论成立的是( )
如图,已知长方形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动,而点R不动时,那么下列结论成立的是( )| A. | 线段EF的长逐渐增大 | B. | 线段EF的长逐渐减少 | ||
| C. | 线段EF的长不变 | D. | 线段EF的长先增大后变小 |
5.已知:$\sqrt{20n}$是整数,则满足条件的最小正整数n的值是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 5 |
6. 如图,AB∥DE,∠ABC=60°,∠CDE=150°,则∠BCD度数为( )
如图,AB∥DE,∠ABC=60°,∠CDE=150°,则∠BCD度数为( )
 如图,AB∥DE,∠ABC=60°,∠CDE=150°,则∠BCD度数为( )
如图,AB∥DE,∠ABC=60°,∠CDE=150°,则∠BCD度数为( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |