题目内容
 如图,AB是⊙O的弦,OP⊥AB交⊙O于C,OC=2,∠ABC=30°.
如图,AB是⊙O的弦,OP⊥AB交⊙O于C,OC=2,∠ABC=30°.(1)求AB的长;
(2)若C是OP的中点,求证:PB是⊙O的切线.
考点:切线的判定
专题:证明题
分析:(1)连接OA、OB,根据圆周角定理得到∠AOC=2∠ABC=60°,则∠OAD=30°,所以OD=
OA=1,AD=
OD=
,再根据垂径定理得AD=BD,所以AB=2
;
(2)由(1)∠BOC=60°,则△OCB为等边三角形,所以BC=OB=OC,∠OBC=∠OCB=60°,而CP=CO=CB,则∠CBP=∠P,可计算出∠CBP=30°,所以∠OBP=∠OBC+∠CBP=90°,于是根据切线的判定定理得PB是⊙O的切线.
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
(2)由(1)∠BOC=60°,则△OCB为等边三角形,所以BC=OB=OC,∠OBC=∠OCB=60°,而CP=CO=CB,则∠CBP=∠P,可计算出∠CBP=30°,所以∠OBP=∠OBC+∠CBP=90°,于是根据切线的判定定理得PB是⊙O的切线.
解答:(1)解: 连接OA、OB,如图,
连接OA、OB,如图,
∵∠ABC=30°,OP⊥AB,
∴∠AOC=60°,
∴∠OAD=30°,
∴OD=
OA=
×2=1,
∴AD=
OD=
,
又∵OP⊥AB,
∴AD=BD,
∴AB=2
;
(2)证明:由(1)∠BOC=60°,
而OC=OB,
∴△OCB为等边三角形,
∴BC=OB=OC,∠OBC=∠OCB=60°,
∴C是OP的中点,
∴CP=CO=CB,
∴∠CBP=∠P,
而∠OCB=∠CBP+∠P,
∴∠CBP=30°
∴∠OBP=∠OBC+∠CBP=90°,
∴OB⊥BP,
∴PB是⊙O的切线.
 连接OA、OB,如图,
连接OA、OB,如图,∵∠ABC=30°,OP⊥AB,
∴∠AOC=60°,
∴∠OAD=30°,
∴OD=
| 1 |
| 2 |
| 1 |
| 2 |
∴AD=
| 3 |
| 3 |
又∵OP⊥AB,
∴AD=BD,
∴AB=2
| 3 |
(2)证明:由(1)∠BOC=60°,
而OC=OB,
∴△OCB为等边三角形,
∴BC=OB=OC,∠OBC=∠OCB=60°,
∴C是OP的中点,
∴CP=CO=CB,
∴∠CBP=∠P,
而∠OCB=∠CBP+∠P,
∴∠CBP=30°
∴∠OBP=∠OBC+∠CBP=90°,
∴OB⊥BP,
∴PB是⊙O的切线.
点评:本题考次了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了垂径定理、圆周角定理和含30度的直角三角形三边的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 平面直角坐标系xOy中,一次函数y=x+n和反比例函数y=-
平面直角坐标系xOy中,一次函数y=x+n和反比例函数y=-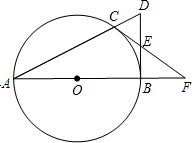 如图,点C是以AB为直径的圆O上一点,直线AC与过点B的切线相交于点D,D点E是BD的中点,直线CE交直线AB与点.求证:
如图,点C是以AB为直径的圆O上一点,直线AC与过点B的切线相交于点D,D点E是BD的中点,直线CE交直线AB与点.求证: 样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:
样调查.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表: 如图,在△ABC和△DEC中,∠BCE=∠ACD,BC=EC,请你添加一个条件,使得△ABC和△DEC全等.并加以证明.你添加的条件是
如图,在△ABC和△DEC中,∠BCE=∠ACD,BC=EC,请你添加一个条件,使得△ABC和△DEC全等.并加以证明.你添加的条件是 将“和谐宜居城市”六个字分别写在一个正方体的六个面上,这个正方体的平面展开图如图,那么在这个正方体中,和“谐”相对的字是( )
将“和谐宜居城市”六个字分别写在一个正方体的六个面上,这个正方体的平面展开图如图,那么在这个正方体中,和“谐”相对的字是( )