题目内容
如图所示是永州八景之一的愚溪桥,桥身横跨愚溪,面临潇水,桥下冬暖夏凉,常有渔船停泊桥下避晒纳凉.已知主桥拱为抛物线型,在正常水位下测得主拱宽24m,最高点离水面8m,以水平线AB为x轴,AB的中点为原点建立坐标系.

(1)求此桥拱线所在抛物线的解析式.
(2)桥边有一浮在水面部分高4m,最宽处12m的渔船,试探索此船能否开到桥下?说明理由.

(1)求此桥拱线所在抛物线的解析式.
(2)桥边有一浮在水面部分高4m,最宽处12m的渔船,试探索此船能否开到桥下?说明理由.
考点:二次函数的应用
专题:
分析:(1)如图可求出A、B、C的坐标,代入函数关系式可得a,b,c的值.
(2)当y=4时求出x的值即可求解.
(2)当y=4时求出x的值即可求解.
解答:解:(1)设抛物线为y=ax2+bx+c
由题意得:A(-12,0),B(12,0),C(0,8).
C点坐标代入得:c=8,
A,B点坐标代入得:
,
解得
.
所求抛物线为y=-
x2+8;
(2)能开到桥下,
理由:当y=4时得
=4,解得:x=±6
高出水面4m处,拱宽12
m>12m(船宽)
所以此船在正常水位时可以开到桥下.
由题意得:A(-12,0),B(12,0),C(0,8).
C点坐标代入得:c=8,
A,B点坐标代入得:
|
解得
|
所求抛物线为y=-
| 1 |
| 18 |
(2)能开到桥下,
理由:当y=4时得
| x2 |
| 18 |
| 2 |
高出水面4m处,拱宽12
| 2 |
所以此船在正常水位时可以开到桥下.
点评:本题考查了二次函数的应用以及以及待定系数法求二次函数解析式,利用图象上点的坐标得出解析式是解题关键.

练习册系列答案
相关题目
天气预报报道某市今天的最高气温35℃,最低气温18℃,则今天宜春市气温的极差是( )
| A、53℃ | B、17℃ |
| C、-17℃ | D、-53℃ |
 如图,P是等边△ABC内的一点,且PA=4,PB=2
如图,P是等边△ABC内的一点,且PA=4,PB=2 如图,在△ABC中,AD为BC边上的中线,DE⊥AB于E,DF⊥AC于F,△ABC面积是60cm2,AB=20cm,AC=16cm,求DE、DF的长.
如图,在△ABC中,AD为BC边上的中线,DE⊥AB于E,DF⊥AC于F,△ABC面积是60cm2,AB=20cm,AC=16cm,求DE、DF的长.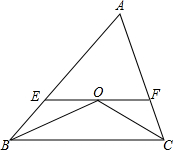 如图,△ABC中,其中AB=7,AC=6,BC=5,∠ABC、∠ACB的平分线交于O点,过O点作BC平行线交AB、AC于E、F,则△AEF的周长为
如图,△ABC中,其中AB=7,AC=6,BC=5,∠ABC、∠ACB的平分线交于O点,过O点作BC平行线交AB、AC于E、F,则△AEF的周长为