题目内容
 如图,P是等边△ABC内的一点,且PA=4,PB=2
如图,P是等边△ABC内的一点,且PA=4,PB=2| 3 |
(1)∠BPC,∠APB的度数;
(2)S△ABC.
考点:旋转的性质,等边三角形的性质,勾股定理的逆定理
专题:计算题
分析:(1)作BH⊥PC于H,如图,根据等边三角形的性质得BA=BC,∠ABC=60°,于是可把△ABP绕点B顺时针旋转60°得到△CBD,连接PD,如图,根据旋转的性质得CD=AP=4,BD=BP=2
,∠PBD=60°,则可判断△PBD为等边三角形,所以PD=PB=2
,∠BPD=60°,然后利用勾股定理的逆定理可证明△PCD为直角三角形,∠CPD=90°,易得∠BPC=150°,利用平角等于有∠BPH=30°,在Rt△PBH中,根据含30度的直角三角形三边的关系可计算出BH=
PB=
,PH=
BH=3,则CH=5;在Rt△BCH中,根据勾股定理计算出BC2=28,则AB2=28,在△ABP中再次利用勾股定理的逆定理可证明△APB为直角三角形,得到∠APB=90°;
(2)根据等边三角形的面积公式求解.
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
(2)根据等边三角形的面积公式求解.
解答:解:(1) 作BH⊥PC于H,如图,
作BH⊥PC于H,如图,
∵△ABC为等边三角形,
∴BA=BC,∠ABC=60°,
∴把△ABP绕点B顺时针旋转60°得到△CBD,连接PD,如图,
∴CD=AP=4,BD=BP=2
,∠PBD=60°,
∴△PBD为等边三角形,
∴PD=PB=2
,∠BPD=60°,
在△PDC中,∵PC=2,PD=2
,CD=4,
∴PC2+PD2=CD2,
∴△PCD为直角三角形,∠CPD=90°,
∴∠BPC=∠BPD+∠CPD=150°,
∴∠BPH=30°,
在Rt△PBH中,∵∠BPH=30°,PB=2
,
∴BH=
PB=
,PH=
BH=3,
∴CH=PC+PH=2+3=5,
在Rt△BCH中,BC2=BH2+CH2=(
)2+52=28,
∴AB2=28,
在△ABP中,∵PB2=(2
)2=12,AP2=42=16,BC2=28,
∴AB2=PA2+PB2,
∴△APB为直角三角形,∠APB=90°,
即∠BPC,∠APB的度数分别为150°,90°;
(2)S△ABC=
BC2=
×28=7
.
 作BH⊥PC于H,如图,
作BH⊥PC于H,如图,∵△ABC为等边三角形,
∴BA=BC,∠ABC=60°,
∴把△ABP绕点B顺时针旋转60°得到△CBD,连接PD,如图,
∴CD=AP=4,BD=BP=2
| 3 |
∴△PBD为等边三角形,
∴PD=PB=2
| 3 |
在△PDC中,∵PC=2,PD=2
| 3 |
∴PC2+PD2=CD2,
∴△PCD为直角三角形,∠CPD=90°,
∴∠BPC=∠BPD+∠CPD=150°,
∴∠BPH=30°,
在Rt△PBH中,∵∠BPH=30°,PB=2
| 3 |
∴BH=
| 1 |
| 2 |
| 3 |
| 3 |
∴CH=PC+PH=2+3=5,
在Rt△BCH中,BC2=BH2+CH2=(
| 3 |
∴AB2=28,
在△ABP中,∵PB2=(2
| 3 |
∴AB2=PA2+PB2,
∴△APB为直角三角形,∠APB=90°,
即∠BPC,∠APB的度数分别为150°,90°;
(2)S△ABC=
| ||
| 4 |
| ||
| 4 |
| 3 |
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的性质与勾股定理的逆定理.

练习册系列答案
相关题目
等边△ABC在数轴上的位置如图所示,点A、C对应的数分别为0和-1,若△ABC绕顶点沿顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1,则连续翻转2015次后,点A( )
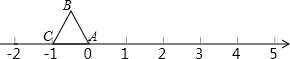
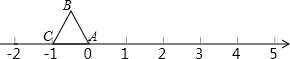
| A、不对应任何数 |
| B、对应的数是2013 |
| C、对应的数是2014 |
| D、对应的数是2015 |
 如图,菱形ABCD中,对角线BD=3,∠BAD=60°,则AC的长为( )
如图,菱形ABCD中,对角线BD=3,∠BAD=60°,则AC的长为( )A、2
| ||
B、3
| ||
C、4
| ||
| D、6 |
 如图,在平面直角坐标系中,A(-1,-3),OB=
如图,在平面直角坐标系中,A(-1,-3),OB=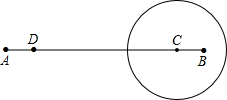 如图,线段AB=8cm,点D从A点出发沿AB向B点匀速运动,速度为1cm/s,同时点C 从B点出发沿BA向A点以相同速度运动,以点C为圆心,2cm长为半径作⊙C,点D到达B点时⊙C也停止运动,设运动时间为t秒,则点D在⊙C内部时t的取值范围是
如图,线段AB=8cm,点D从A点出发沿AB向B点匀速运动,速度为1cm/s,同时点C 从B点出发沿BA向A点以相同速度运动,以点C为圆心,2cm长为半径作⊙C,点D到达B点时⊙C也停止运动,设运动时间为t秒,则点D在⊙C内部时t的取值范围是
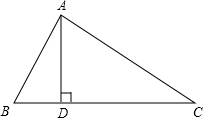 在△ABC中,AD是BC边上的高,CD=AB+BD.求证:∠B=2∠C.
在△ABC中,AD是BC边上的高,CD=AB+BD.求证:∠B=2∠C.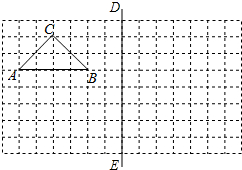 如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题:
如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题: