题目内容
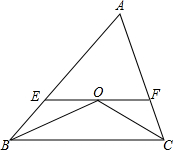如图，△ABC中，其中AB=7，AC=6，BC=5，∠ABC、∠ACB的平分线交于O点，过O点作BC平行线交AB、AC于E、F，则△AEF的周长为考点：等腰三角形的判定与性质,平行线的性质
专题：
分析：根据∠ABC和∠ACB的平分线相交于点O，过点O作BC的平行线交AB于点E，可证∠EOB=∠EBO，可得BE=EO，OF=FC，然后利用AB+AC即可求出△AEF的周长．
解答：解：∵BO是∠ABC的平分线，
∴∠EBO=∠OBC，
∵过点O作BC的平行线交AB于点E，
∴∠EOB=∠OBC，
∴∠EOB=∠EBO，
∴BE=EO，
同理可得OF=FC，
∴△AEF的周长即为AB+AC=7+6=13．
故答案为：13．
∴∠EBO=∠OBC，
∵过点O作BC的平行线交AB于点E，
∴∠EOB=∠OBC，
∴∠EOB=∠EBO，
∴BE=EO，
同理可得OF=FC，
∴△AEF的周长即为AB+AC=7+6=13．
故答案为：13．
点评：此题主要考查等腰三角形的判定与性质和平行线的性质，此题的突破点是△AEF的周长即为AB+AC．
练习册系列答案
相关题目
如图，在所给网格图（每小格均为边长是1的正方形）中完成下列各题：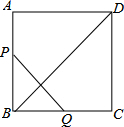
如图，在矩形ABCD中，∠C=90°，AB=6cm，BC=8cm，点P、Q分别是AB、BC边上的动点．若点P以1cm/s的速度从A出发向点B运动，点Q以2cm/s的速度从点B出发向点C运动，且两点同时出发，问：出发时间为多少秒时△BCD与△PBQ相似？