题目内容
12.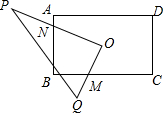 如图,矩形ABCD中,AB=4,AD=6,O为矩形ABCD的中心,将直角三角形的直角顶点与O重合,一条直角边OP与OA重合,使三角板沿逆时针方向绕点O旋转,两条直角边始终与边BC、AB相交,交点分别为M、N.若BM=x,AN=y,则y与x之间的函数关系式是y=$\frac{3}{2}$x-$\frac{5}{2}$.
如图,矩形ABCD中,AB=4,AD=6,O为矩形ABCD的中心,将直角三角形的直角顶点与O重合,一条直角边OP与OA重合,使三角板沿逆时针方向绕点O旋转,两条直角边始终与边BC、AB相交,交点分别为M、N.若BM=x,AN=y,则y与x之间的函数关系式是y=$\frac{3}{2}$x-$\frac{5}{2}$.
分析 过点O分别作OF⊥AB与F,OE⊥BC与E,易证明△NOF∽△MOE,利用相似比作为相等关系即可得到关于x,y的方程,整理即可得到函数关系式.
解答 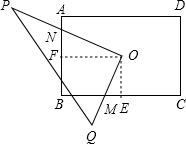 解:过点O分别作OF⊥AB与F,OE⊥BC与E
解:过点O分别作OF⊥AB与F,OE⊥BC与E
∵∠POQ=∠EOF=90°
∴∠NOF=∠MOE
∵∠NFO=∠MEO=90°
∴△NOF∽△MOE
∴$\frac{NF}{OF}=\frac{ME}{OE}$,
∵AB=4,AD=6,BM=x,AN=y
∴NF=2-y,ME=3-x,OF=3,OE=2
∴$\frac{2-y}{3}=\frac{3-x}{2}$
∴y=$\frac{3}{2}$x-$\frac{5}{2}$(0<x<6).
故答案为:y=$\frac{3}{2}$x-$\frac{5}{2}$.
点评 本题考查了相似三角形的判定和性质,求函数的解析式,矩形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.为了满足学生的物质需求,重庆市某重点中学到mama超市准备购进甲、乙两种绿色袋装食品.其中甲、乙两种绿色袋装食品的进价和售价如下表:
已知:用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同.
(1)求m的值;
(2)要使购进的甲、乙两种绿色袋装食品共800袋的总利润(利润=售价-进价)不少于5200元,且不超5280元,问该mama超市有几种进货方案?
(3)在(2)的条件下,该mama超市准备对甲种袋装食品进行优惠促销活动,决定对甲种袋装食品每袋优惠a(2<a<7)元出售,乙种袋装食品价格不变.那么该mama超市要获得最大利润应如何进货?
| 甲 | 乙 | |
| 进价(元/袋) | m | m-2 |
| 售价(元/袋) | 20 | 13 |
(1)求m的值;
(2)要使购进的甲、乙两种绿色袋装食品共800袋的总利润(利润=售价-进价)不少于5200元,且不超5280元,问该mama超市有几种进货方案?
(3)在(2)的条件下,该mama超市准备对甲种袋装食品进行优惠促销活动,决定对甲种袋装食品每袋优惠a(2<a<7)元出售,乙种袋装食品价格不变.那么该mama超市要获得最大利润应如何进货?
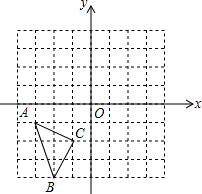 在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标(-3,-1),
在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标(-3,-1),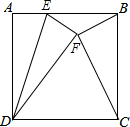 如图,已知E是正方形ABCD的边AB上一点,点A关于DE的对称点为F,∠BFC=90°,求$\frac{AB}{AE}$的值.
如图,已知E是正方形ABCD的边AB上一点,点A关于DE的对称点为F,∠BFC=90°,求$\frac{AB}{AE}$的值.
 走进每一家医院,我们总会看到这个图标(如图),图标中的线段AB平移后能得到线段EF.
走进每一家医院,我们总会看到这个图标(如图),图标中的线段AB平移后能得到线段EF. 如图,?ABCD,AB=6,AD=9,BE平分∠ABC,交AD于点E,交CD延长线于点F,则DF的长等于( )
如图,?ABCD,AB=6,AD=9,BE平分∠ABC,交AD于点E,交CD延长线于点F,则DF的长等于( )