题目内容
6. 如图,将边长为6的正方形ABCO放置在直角坐标系中,使点A在x轴负半轴上,点C在y轴正半轴上.点M(t,0)在x轴上运动,过A作直线MC的垂线交y轴于点N.
如图,将边长为6的正方形ABCO放置在直角坐标系中,使点A在x轴负半轴上,点C在y轴正半轴上.点M(t,0)在x轴上运动,过A作直线MC的垂线交y轴于点N.(1)当t=2时,tan∠NAO=$\frac{1}{3}$;
(2)在直角坐标系中,取定点P(3,8),则在点M运动过程中,当以M、N、C、P为顶点的四边形是梯形时,点M的坐标为(3,0)或(4+$\sqrt{34}$,0)或(4-$\sqrt{34}$,0).
分析 (1)根据余角的定义,可得∠CMO+∠NAO,∠CMO+∠MCO,根据余角的性质,可得∠NAO=∠MCO,根据等角的三角函数值相等,可得tan∠NAO的值;
(2)分别从CN∥PM与PN∥CM(当M在x轴正半轴与负半轴)时,去分析求解,注意利用相似三角形的对应边成比例,即可求得答案.
解答 解:(1)∵AN⊥CM,
∴∠CMO+∠NAO=90°.
∵四边形ABCO是正方形,
∴∠AOC=90°,
∴∠CMO+∠MCO=90°.
∴∠NAO=∠MCO.
∴tan∠NAO=tan∠MCO=$\frac{MO}{CO}$=$\frac{2}{6}$=$\frac{1}{3}$;
(2)①如图1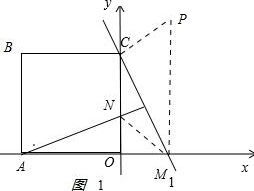 ,
,
当CN∥PM时,
∵P(3,8),
∴M1(3,0);
②如图2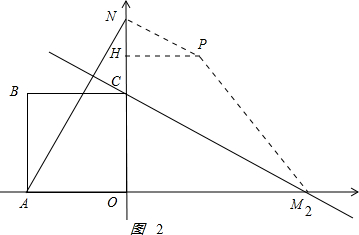 ,
,
当PN∥CM时,
则∠PNH=∠MCO,
过点P作PH⊥ON于H,
则∠PHN=∠MOC=90°,
则△PHN∽△MOC,
故$\frac{PH}{OM}$=$\frac{NH}{OC}$,
设点M(a,0),则N(0,a)(a>0),
则NH=a-8,PH=3,OC=6,OM=a,
故$\frac{3}{a}$=$\frac{a-8}{6}$,
解得:a=4+$\sqrt{34}$;
故M2(4+$\sqrt{34}$,0);
③如图3,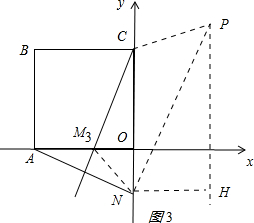 ,
,
当CM∥PN时,
则∠PNH=∠CMO,
过点P作PH⊥ON于H,
则∠PHN=∠COM=90°,
则△PHN∽△COM,
故$\frac{PH}{OC}$=$\frac{NH}{OM}$,
设点M(-b,0),则N(0,-b)(b>0),
则NH=3,PH=8+b,OC=6,OM=b,
则$\frac{8+b}{6}$=$\frac{3}{b}$,
解得:b=$\sqrt{34}$-4;
故M2(4-$\sqrt{34}$,0).
故点M的坐标为(3,0)或(4+$\sqrt{34}$,0)或(4-$\sqrt{34}$,0).
故答案为:(1)$\frac{1}{3}$;(2)(3,0)或(4+$\sqrt{34}$,0)或(4-$\sqrt{34}$,0).
点评 此题考查了一次函数综合题,利用了正方形的性质、梯形的性质、相似三角形的判定与性质、全等三角形的判定与性质以及三角函数的定义等知识.此题难度较大,注意掌握数形结合思想、分类讨论思想与方程思想的应用,注意辅助线的作法.

 阅读下面一段材料,运用相关知识解决问题.
阅读下面一段材料,运用相关知识解决问题.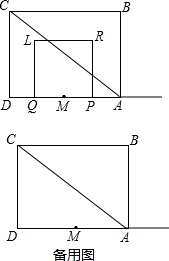 如图,四边形ABCD为矩形,AC为对角线,AB=6,BC=8,点M是AD的中点,P、Q两点同时从点M出发,点P沿射线MA向右运动;点Q沿线段MD先向左运动至点D后,再向右运动到点M停止,点P随之停止运动.P、Q两点运动的速度均为每秒1个单位.以PQ为一边向上作正方形PRLQ.设点P的运动时间为t(秒),正方形PRLQ与△ABC重叠部分的面积为S.
如图,四边形ABCD为矩形,AC为对角线,AB=6,BC=8,点M是AD的中点,P、Q两点同时从点M出发,点P沿射线MA向右运动;点Q沿线段MD先向左运动至点D后,再向右运动到点M停止,点P随之停止运动.P、Q两点运动的速度均为每秒1个单位.以PQ为一边向上作正方形PRLQ.设点P的运动时间为t(秒),正方形PRLQ与△ABC重叠部分的面积为S.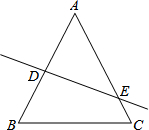 如图,己知AB=AC,DE垂直平分AB交AB于E点,若AB=12cm,BC=10cm,∠BAC=40°,求△BCE的周长和∠EBC的度数.
如图,己知AB=AC,DE垂直平分AB交AB于E点,若AB=12cm,BC=10cm,∠BAC=40°,求△BCE的周长和∠EBC的度数.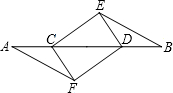 如图,已知AF∥BE,且AF=BE,AC=BD.请指出图中有哪些全等三角形,并任选一对给予证明.
如图,已知AF∥BE,且AF=BE,AC=BD.请指出图中有哪些全等三角形,并任选一对给予证明.