题目内容
1.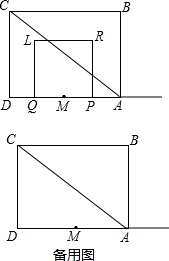 如图,四边形ABCD为矩形,AC为对角线,AB=6,BC=8,点M是AD的中点,P、Q两点同时从点M出发,点P沿射线MA向右运动;点Q沿线段MD先向左运动至点D后,再向右运动到点M停止,点P随之停止运动.P、Q两点运动的速度均为每秒1个单位.以PQ为一边向上作正方形PRLQ.设点P的运动时间为t(秒),正方形PRLQ与△ABC重叠部分的面积为S.
如图,四边形ABCD为矩形,AC为对角线,AB=6,BC=8,点M是AD的中点,P、Q两点同时从点M出发,点P沿射线MA向右运动;点Q沿线段MD先向左运动至点D后,再向右运动到点M停止,点P随之停止运动.P、Q两点运动的速度均为每秒1个单位.以PQ为一边向上作正方形PRLQ.设点P的运动时间为t(秒),正方形PRLQ与△ABC重叠部分的面积为S.(1)当点R在线段AC上时,求出t的值.
(2)求出S与t之间的函数关系式,并直接写出取值范围.(求函数关系式时,只须写出重叠部分为三角形时的详细过程,其余情况直接写出函数关系式.)
(3)在点P、点Q运动的同时,有一点E以每秒1个单位的速度从C向B运动,当t为何值时,△LRE是等腰三角形.请直接写出t的值或取值范围.
分析 (1)根据三角形相似可得$\frac{RP}{AP}=\frac{CD}{AD}$,即$\frac{2t}{4-t}=\frac{6}{8}$,解答即可;
(2)根据点P和点Q的运动情况分情况讨论解答即可;
(3)根据△LRE是等腰三角形满足的条件.
解答 解:(1)当点R在线段AC上时,应该满足:$\frac{RP}{AP}=\frac{DC}{AD}$,
设MP为t,则PR=2t,AP=4-t,
∴可得:$\frac{RP}{AP}=\frac{CD}{AD}$,即$\frac{2t}{4-t}=\frac{6}{8}$,
解得:t=$\frac{12}{11}$;
(2)当$0<t≤\frac{12}{11}$时,正方形PRLQ与△ABC没有重叠部分,所以重叠部分的面积为0;
当$\frac{12}{11}<t≤\frac{12}{5}$时,正方形PRLQ与△ABC重叠部分的面积为直角三角形KRW的面积=$\frac{1}{2}×(\frac{11}{4}t-3)×\frac{4}{3}×(\frac{11}{4}t-3)=\frac{121}{24}{t}^{2}-11t+6$,
$S=\frac{121}{24}{t}^{2}-11t+6$;
当$\frac{12}{5}<t≤3$时,正方形PRLQ与△ABC重叠部分的面积=$\frac{1}{2}$×[2t-$\frac{3}{4}$(4+t)+2t-$\frac{3}{4}$(4-t)]•2t=4t2-6t.
当3<t≤4时,正方形PRLQ与△ABC重叠部分的面积=$\frac{1}{2}$×(12-2t)×2t=-2t2+12t.
当4<t≤8时,正方形PRLQ与△ABC重叠部分的面积为S=$-\frac{3}{8}{t}^{2}+3t+18$;
综上所述S与t之间的函数关系式为:S=$\left\{\begin{array}{l}{0}&{(0<t≤\frac{12}{11})}\\{\frac{121}{24}{t}^{2}-11t+6}&{(\frac{12}{11}<t≤\frac{12}{5})}\\{4{t}^{2}-6t}&{(\frac{12}{5}<t≤3)}\\{-2{t}^{2}+12t}&{(3<t≤4)}\\{-\frac{3}{8}{t}^{2}+3t+18}&{(4<t≤8)}\end{array}\right.$.
(3)在点P、点Q运动的同时,有一点E以每秒1个单位的速度从C向B运动,
①当点E是BC的中点时,点E在LR的中垂线线上时,EL=ER.此时t=4s,△LRE是等腰三角形;
当点E与点B重合时,点E在LR的中垂线线上时,EL=ER.此时t=8s,△LRE是等腰三角形;
综上所述,t的取值范围是4≤t≤8;
②当EL=LR时,如图所示:
LR=2t,CF=NL=4-t,则EF=2t-4.FL=CN=6-2t,
则在直角△EFL中,由勾股定理得到:EL2=EF2+FL2=(2t-4)2+(6-2t)2.
故由EL=LR得到:EL2=LR2,即4t2=10t2-40t+52,
整理,得
t2-10t+13=0,
解得 t1=5+2$\sqrt{3}$(舍去),t2=5-2$\sqrt{3}$.
所以当t=5-2$\sqrt{3}$(s)时,△LRE是等腰三角形;
同理,当ER=LR时,$t=\frac{13}{6}$.
综上所述,t的取值范围是4≤t≤8时,△LRE是等腰三角形;当t=4s,或t=8s或$t=\frac{13}{6}$s或$t=5-2\sqrt{3}$s时,△LRE是等腰三角形.
点评 本题是矩形的判定和性质以及三角形中的动点问题,解决问题时,一定要变动为静,将其转化为常见的几何问题,再进行解答.

 天天练口算系列答案
天天练口算系列答案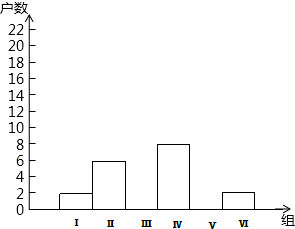 今年是我国施行“清明”小长假的第二年,在长假期间,某校团委要求学生参加一项社会调查活动.九年级学生小青想了解她所居住的小区500户居民的家庭人均收入情况,从中随机调查了40户居民家庭的人均收入情况(收入取整数,单位:元)并绘制了如下的分布表和分布图:
今年是我国施行“清明”小长假的第二年,在长假期间,某校团委要求学生参加一项社会调查活动.九年级学生小青想了解她所居住的小区500户居民的家庭人均收入情况,从中随机调查了40户居民家庭的人均收入情况(收入取整数,单位:元)并绘制了如下的分布表和分布图:| 分组 | 户数 | 百分比 |
| Ⅰ:600-799 | 2 | 0.05 |
| Ⅱ:800-999 | 6 | 0.15 |
| Ⅲ:1000-1199 | 0.45 | |
| Ⅳ:1200-1399 | 8 | 0.20 |
| Ⅴ:1400-1599 | ||
| Ⅵ:1600-1800 | 2 | 0.05 |
| 合计 | 40 | 1.00 |
(1)补全分布表、分布图;
(2)这40户家庭收入的中位数落在哪一个小组?
(3)被调查的家庭中,参加“清明扫墓“活动的家庭统计如表:
| 收入情况 | 600-799 | 800-999 | 1000-1199 | 1200-1399 | 1400-1599 | 1600-1800 |
| $\frac{参加扫墓家庭数}{被调查家庭数}$ | $\frac{1}{2}$ | $\frac{1}{3}$ | $\frac{1}{6}$ | $\frac{1}{4}$ | 1 | 1 |
 已知,如图,AB=AC,点D,E分别是AC,AB的中点,求证:△ABD≌△ACE.
已知,如图,AB=AC,点D,E分别是AC,AB的中点,求证:△ABD≌△ACE. 在长方形ABCD中,AB=30cm,BC=40cm,如图,P为BC上一点,PQ⊥AC,PR⊥BD,求PQ+PR的值.
在长方形ABCD中,AB=30cm,BC=40cm,如图,P为BC上一点,PQ⊥AC,PR⊥BD,求PQ+PR的值. 如图,将边长为6的正方形ABCO放置在直角坐标系中,使点A在x轴负半轴上,点C在y轴正半轴上.点M(t,0)在x轴上运动,过A作直线MC的垂线交y轴于点N.
如图,将边长为6的正方形ABCO放置在直角坐标系中,使点A在x轴负半轴上,点C在y轴正半轴上.点M(t,0)在x轴上运动,过A作直线MC的垂线交y轴于点N.