题目内容
15.已知关于x的一元二次方程mx2-2(3m-1)x+9m=1有两个实数根,求实数m的取值范围.分析 先把方程化为一元二次方程的一般形式,再根据方程有两个实数根与一元二次方程的定义列出关于m的方程组,求出m的值即可.
解答 解:原方程可化为mx2-2(3m-1)x+9m-1=0,
∵此方程有两个相等的实数根,
∴△=0,即△=4(3m-1)2-4m(9m-1)≥0,
∴$\left\{\begin{array}{l}m≠0\\ 4{(3m-1)}^{2}-4m(9m-1)≥0\end{array}\right.$,解得m≤$\frac{1}{5}$且m≠0.
点评 本题考查的是根的判别式,熟知一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac的关系是解答此题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
 对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+$\frac{b}{k}$,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.例如:P(2,4)的“2属派生点”为P′(2+$\frac{4}{2}$,2×2+4),即P′(4,8).
对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+$\frac{b}{k}$,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.例如:P(2,4)的“2属派生点”为P′(2+$\frac{4}{2}$,2×2+4),即P′(4,8). 如图,将边长为6的正方形ABCO放置在直角坐标系中,使点A在x轴负半轴上,点C在y轴正半轴上.点M(t,0)在x轴上运动,过A作直线MC的垂线交y轴于点N.
如图,将边长为6的正方形ABCO放置在直角坐标系中,使点A在x轴负半轴上,点C在y轴正半轴上.点M(t,0)在x轴上运动,过A作直线MC的垂线交y轴于点N.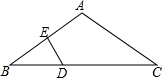 已知:如图,在△ABC中,AB=AC,∠BAC=120°,DE⊥AB,且BE=AE.求证:DC=2BD.
已知:如图,在△ABC中,AB=AC,∠BAC=120°,DE⊥AB,且BE=AE.求证:DC=2BD.