题目内容
14.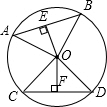 如图,AB,CD是⊙O的两条弦.
如图,AB,CD是⊙O的两条弦.(1)如果AB=CD,那么$\widehat{AB}$=$\widehat{CD}$,∠AOB=∠COD.
(2)如果$\widehat{AB}$=$\widehat{CD}$,那么∠AOB=∠COD,AB=CD.
(3)如果∠AOB=∠COD,那么$\widehat{AB}$=$\widehat{CD}$,AB=CD.
(4)如果AB=CD,OE⊥AB于点E,OF⊥CD于点F,OE与OF相等吗?为什么?
分析 (1)、(2)、(3)利用圆心角、弧、弦的关系直接求解;
(4)先利用垂径定理得到AE=BE,CF=DF,而AB=CD,则AE=CF,然后利用勾股定理可判断OE=OF.
解答 解:(1)如果AB=CD,那么$\widehat{AB}$=$\widehat{CD}$,∠AOB=∠COD;
(2)如果$\widehat{AB}$=$\widehat{CD}$,那么∠AOB=∠COD;AB=CD;
(3)如果∠AOB=∠COD,那么$\widehat{AB}$=$\widehat{CD}$,AB=CD;
(4)OE与OF相等.利用如下:
∵OE⊥AB于点E,OF⊥CD于点F,
∴AE=BE,CF=DF,
而AB=CD,
∴AE=CF,
∵OF=$\sqrt{O{A}^{2}-A{E}^{2}}$,OF=$\sqrt{O{C}^{2}-C{F}^{2}}$,
∴OE=OF.
故答案为$\widehat{AB}$=$\widehat{CD}$,∠AOB=∠COD;∠AOB=∠COD,AB=CD;$\widehat{AB}$=$\widehat{CD}$,AB=CD.
点评 本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.也考查了垂径定理.

练习册系列答案
相关题目
5.P(3,-4)与点M(a,b)关于原点对称,则a+b的值为( )
| A. | -1 | B. | 1 | C. | 3 | D. | -4 |
9.甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9;
乙:5,9,7,10,9.
(1)填写表格:
(2)根据这5次成绩,你认为推荐谁参加射击比赛更合适,请说明理由.
甲:8,8,7,8,9;
乙:5,9,7,10,9.
(1)填写表格:
| 平均数 | 众数 | 中位数 | 方差 | |
| 甲 | 8 | 8 | 8 | 0.4 |
| 乙 | 8 | 9 | 9 | 3.2 |
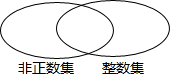 如图的两个圈分别表示非正数集和整数集,请在每个圈内填入六个数,其中三个数既在非正数集又在整数集内,你能用一个合适的语句来表示两个圈重叠部分的意义吗?
如图的两个圈分别表示非正数集和整数集,请在每个圈内填入六个数,其中三个数既在非正数集又在整数集内,你能用一个合适的语句来表示两个圈重叠部分的意义吗?