题目内容
4.在直角坐标系中,不论a取何值,抛物线y=-$\frac{1}{2}$x2$+\frac{5-a}{2}$x+2a-2经过x轴上一定点Q,直线y=(a-2)x+2经过点Q.求抛物线的解析式.分析 根据题意求得Q的坐标,然后代入y=(a-2)x+2求得a的值,即可求得抛物线的解析式.
解答 解:∵不论a取何值,抛物线y=-$\frac{1}{2}$x2$+\frac{5-a}{2}$x+2a-2经过x轴上一定点Q,
∴当a=0,则y=-$\frac{1}{2}$x2+$\frac{5}{2}$x-2,当a=1时y=-$\frac{1}{2}$x2+2x,
令y=0,则-$\left\{\begin{array}{l}{-\frac{1}{2}{x}^{2}+\frac{5}{2}x-2=0}\\{-\frac{1}{2}{x}^{2}+2x=0}\end{array}\right.$
解得x=4,
∴Q(4,0),
∵直线y=(a-2)x+2经过点Q.
∴0=(a-2)×4+2,
解得a=$\frac{3}{2}$,
∴抛物线的解析式为y=-$\frac{1}{2}$x2+$\frac{7}{4}$x+1.
点评 本题考查了待定系数法求二次函数的解析式以及一次函数图象上点的坐标特征,求得Q点的坐标是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
14.把抛物线y=x2+1向右平移3个单位,再向上平移2个单位,得到抛物线( )
| A. | y=(x+3)2-1 | B. | y=(x+3)2+3 | C. | y=(x-3)2-1 | D. | y=(x-3)2+3 |
15.下列计算正确的是( )
| A. | 2a-a=2 | B. | m6÷m2=m3 | ||
| C. | x2010+x2010=2x2010 | D. | t2•t3=t6 |
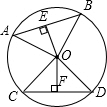 如图,AB,CD是⊙O的两条弦.
如图,AB,CD是⊙O的两条弦.