题目内容
先化简,再求值
(1)(
+
)÷
,其中x=2.
(2)(
-
)÷
,其中x满足x2-x-1=0.
(1)(
| 1 |
| x+1 |
| x2-2x+1 |
| x2-1 |
| x-1 |
| x+1 |
(2)(
| x-1 |
| x |
| x-2 |
| x+1 |
| 2x2-x |
| x2+2x+1 |
考点:分式的化简求值
专题:计算题
分析:(1)原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把已知等式变形后代入计算即可求出值.
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把已知等式变形后代入计算即可求出值.
解答:解:(1)原式=
•
=
•
=
,
当x=2时,原式=2;
(2)原式=
•
=
,
由x2-x-1=0,得到x2=x+1,
则原式=1.
| x-1+x2-2x+1 |
| (x+1)(x-1) |
| x+1 |
| x-1 |
| x(x-1) |
| (x+1)(x-1) |
| x+1 |
| x-1 |
| x |
| x-1 |
当x=2时,原式=2;
(2)原式=
| x2-1-x2+2x |
| x(x+1) |
| (x+1)2 |
| x(2x-1) |
| x+1 |
| x2 |
由x2-x-1=0,得到x2=x+1,
则原式=1.
点评:此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 如图,已知双曲线y=
如图,已知双曲线y=| k1 |
| x |
| 3 |
| 2 |
(1)求双曲线和直线的解析式;
(2)直接写出使
| k1 |
| x |
若化简|1-x|-
的结果是2x-4,则x的取值范围是( )
| x2-6x+9 |
| A、x≤3 | B、x≥1 |
| C、1≤x≤3 | D、1<x<3 |
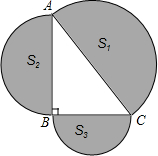 如图,在Rt△ABC中,∠ABC=90°,分别以AC、AB、BC为直径,在△ABC外作半圆,若S1=6,则S2+S3的值为
如图,在Rt△ABC中,∠ABC=90°,分别以AC、AB、BC为直径,在△ABC外作半圆,若S1=6,则S2+S3的值为 如图,AM平分∠BAD,CM平分∠BCD
如图,AM平分∠BAD,CM平分∠BCD