题目内容
18.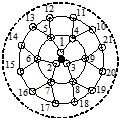 课题研究小组对附着在物体表面的三个微生物(课题小组成员把他们分别标号为1,2,3)的生长情况进行观察记录.这三个微生物第一天各自一分为二,产生新的微生物(分别被标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物(课题组成员用如图所示的图形进行形象的记录).那么标号为150的微生物会出现在( )
课题研究小组对附着在物体表面的三个微生物(课题小组成员把他们分别标号为1,2,3)的生长情况进行观察记录.这三个微生物第一天各自一分为二,产生新的微生物(分别被标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物(课题组成员用如图所示的图形进行形象的记录).那么标号为150的微生物会出现在( )| A. | 第3天 | B. | 第4天 | C. | 第5天 | D. | 第6天 |
分析 设第n天有an个微生物,第n天标号最大为Sn,由微生物的分裂性质可得出an=3×2n,通过计算找出Sn=an+1-a1=3×(2n+1-1),由此即可得出结论.
解答 解:设第n天有an个微生物,第n天标号最大为Sn,
观察,发现规律:a0=3,a1=2a0=6,a2=2a1=12,a3=2a2=24,…,
∴an=3×2n.
∵Sn=a1+a2+a3+…+an,2Sn=a2+a3+…+an+an+1,
∴Sn=an+1-a1=3×(2n+1-1).
∵当n=4时,S4=3×(25-1)=93;
当n=5时,S5=3×(26-1)=189.
93<150<189,
∴标号为150的微生物会出现在第5天.
故选C.
点评 本题考查了规律型中的数字的变化类,解题的关键是找出第n天标号最大为Sn=3×(2n+1-1).本题属于中档题,难度不大,解决该题型题目时,根据给定数据找出变化规律是关键.解决该题时,由于初中未学过等比数列的求和公式,此处用到了错位想减法寻找等比数列的前n项和.

练习册系列答案
相关题目
8.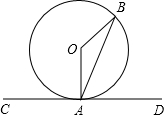 如图,AB是⊙O的弦,CD与⊙O相切于点A,若∠BAD=66°,则∠B等于( )
如图,AB是⊙O的弦,CD与⊙O相切于点A,若∠BAD=66°,则∠B等于( )
 如图,AB是⊙O的弦,CD与⊙O相切于点A,若∠BAD=66°,则∠B等于( )
如图,AB是⊙O的弦,CD与⊙O相切于点A,若∠BAD=66°,则∠B等于( )| A. | 24° | B. | 33° | C. | 48° | D. | 66° |
9.已知∠α=30°,那么∠α的余角等于( )
| A. | 30° | B. | 60° | C. | 70° | D. | 150° |
3.下列几何体中,主视图是圆的是( )
| A. |  圆柱 | B. |  圆锥 | C. |  球 | D. |  立方体 |
10.已知,函数y=$\frac{k}{x}$的图象经过点(-1,2),则函数y=kx+2的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,在平行四边形ABCD中,AB=6,BC=4,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将平行四边形ABCD沿EF折叠,得到四边形EFGH,点A的对应点为点C,点D的对应点为点G.则△CEF的面积$\frac{7\sqrt{3}}{2}$.
如图,在平行四边形ABCD中,AB=6,BC=4,∠B=60°,点E是边AB上的一点,点F是边CD上一点,将平行四边形ABCD沿EF折叠,得到四边形EFGH,点A的对应点为点C,点D的对应点为点G.则△CEF的面积$\frac{7\sqrt{3}}{2}$.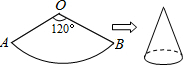 如图,一个扇形铁皮OAB,已知OA=12cm,∠AOB=120°,小华将OA、OB合拢制成了一个圆锥形烟囱帽(接缝处忽略不计),则烟囱帽的高为8$\sqrt{2}$cm.
如图,一个扇形铁皮OAB,已知OA=12cm,∠AOB=120°,小华将OA、OB合拢制成了一个圆锥形烟囱帽(接缝处忽略不计),则烟囱帽的高为8$\sqrt{2}$cm.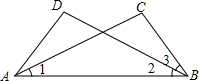 已知,如图,AC=BD,∠1=∠2.
已知,如图,AC=BD,∠1=∠2.