题目内容
11.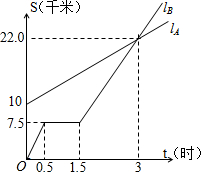 如图,lA lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
如图,lA lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.(1)B出发时与A相距10千米.
(2)走了一段路后,自行车发生故障,进行修理,所用的时间是1小时.
(3)B出发后3小时与A相遇.
(4)若B的自行车不发生故障,保持出发时速度前进,$\frac{10}{11}$小时与A相遇,相遇点离B的出发点$\frac{150}{11}$千米(写出过程)
分析 (1)从图上可看出B出发时与A相距10千米.
(2)修理的时间就是路程不变的时间是1.5-0.5=1小时.
(3)从图象看出3小时时,两个图象相交,所以3小时时相遇.
(4)根据题意分别得出lA与 lB的解析式,进而求出相遇时的时间和相遇时的距离.
解答 解:(1)由图形可得B出发时与A相距10千米;
(2)在图中发现0.5至1.5小时,自行车没有行走,
故可得出修理所用的时间为1小时.
(3)图中两直线的交点是B与A相遇的时刻,
即出发3小时后与A相遇.
(4)设lA 函数是为S=kt+b,且过(0,10)和(3,22),
则$\left\{\begin{array}{l}{b=10}\\{3k+b=22}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=4}\\{b=10}\end{array}\right.$.
故S与时间t的函数关系式为:S=4t+10.
设lB的解析式为:S=at,又过点(0.5,7.5),
则7.5=0.5a,
解得:a=15,
故S=15t;
解方程组$\left\{\begin{array}{l}{S=4t+10}\\{S=15t}\end{array}\right.$ 得$\left\{\begin{array}{l}{t=\frac{10}{11}}\\{S=\frac{150}{11}}\end{array}\right.$,
即经过$\frac{10}{11}$小时与A相遇,相遇点离B的出发点$\frac{150}{11}$千米.
故答案为10,1,3,$\frac{10}{11}$,$\frac{150}{11}$.
点评 此题主要考查了一次函数的应用,根据题中已知图象得出点的坐标求出解析式是解题关键.

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案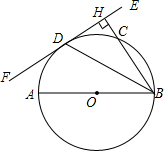 如图,AB为⊙O的直径,D是⊙O上一点,过D点作直线EF,BH⊥EF交⊙O于点C,垂足为H,且BD平分∠ABH.
如图,AB为⊙O的直径,D是⊙O上一点,过D点作直线EF,BH⊥EF交⊙O于点C,垂足为H,且BD平分∠ABH.(1)求证:EF是⊙O的切线;
(2)如果AB=12,BC=8,求圆心O到BC的距离.
 ,则其运算结果为( )
,则其运算结果为( )| A. | -8 | B. | -6 | C. | 6 | D. | 8 |
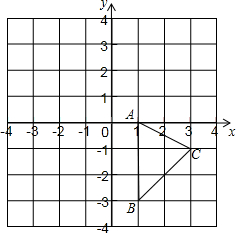 如图,平面直角坐标系中,△ABC的顶点都在网格点上,其中点A坐标为(1,0)
如图,平面直角坐标系中,△ABC的顶点都在网格点上,其中点A坐标为(1,0)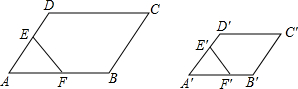 如图,?ABCD∽?A′B′C′D′,E、F分别是DA、AB的中点,E′、F′分别是D′A′、A′B′的中点,求证:五边形BCDEF∽五边形B′C′D′E′F′.
如图,?ABCD∽?A′B′C′D′,E、F分别是DA、AB的中点,E′、F′分别是D′A′、A′B′的中点,求证:五边形BCDEF∽五边形B′C′D′E′F′. 如图,在线段AB上有一点C,若AC:CB=CB:AB,则称点C为AB的黄金分割点,现已知AB=1,点C是线段AB的黄金分割点(AC<BC),求BC的长.
如图,在线段AB上有一点C,若AC:CB=CB:AB,则称点C为AB的黄金分割点,现已知AB=1,点C是线段AB的黄金分割点(AC<BC),求BC的长.