题目内容
13.在同一坐标系中,函数y=$\frac{k}{x}$ 和y=kx-k的图象大致是( )| A. |  | B. |  | C. |  | D. | .K] |
分析 根据四个选项中的一次函数的图象依据一次函数图象与系数的关系可得出k的取值范围,由此得出A、C不正确,再分析B、D中的反比例函数图象即可得出结论.
解答 解:A、由一次函数图象可知:k>0,-k>0,
∴A不正确;
B、由一次函数图象可知:k>0,-k<0,
由反比例函数图象可知:k>0,
∴B正确;
C、由一次函数图象可知:k<0,-k<0,
∴C不正确;
D、由一次函数图象可知:k<0,-k>0,
由反比例函数图象可知:k>0,
∴D不正确.
故选B.
点评 本题考查了反比例函数的性质以及一次函数图象与系数的关系,解题的关键是逐项分析k的取值范围.本题属于基础题,难度不大,解决该题型题目时,根据一次函数的图象结合一次函数图象与系数的关系找出系数k的取值范围是关键.

练习册系列答案
相关题目
3.下列各方程组中,属于二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{x+2y=3}\\{x-z=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x-3y=6}\\{xy=5}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{\frac{x}{2}+\frac{y}{3}=4}\\{4x+3y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{2}{x}+\frac{y}{3}=\frac{1}{2}}\\{x+2y=3}\end{array}\right.$ |
4.矩形的对角线长为20,两邻边之比为3:4,则矩形的面积为( )
| A. | 56 | B. | 192 | C. | 20 | D. | 以上答案都不对 |
1.下列计算正确是( )
| A. | a3+a2=a5 | B. | a8÷a4=a2 | C. | (a4)2=a8 | D. | (-a)3(-a)2=a5 |
18. 如图,在?ABCD中,BC=BD,∠C=65°,则∠ADB的度数是( )
如图,在?ABCD中,BC=BD,∠C=65°,则∠ADB的度数是( )
 如图,在?ABCD中,BC=BD,∠C=65°,则∠ADB的度数是( )
如图,在?ABCD中,BC=BD,∠C=65°,则∠ADB的度数是( )| A. | 25° | B. | 35° | C. | 50° | D. | 60° |
5.关于x的一元二次方程x2-2x+k=0有两个实数根,则实数k的取值范围是( )
| A. | k≤1 | B. | k>1 | C. | k=1 | D. | k≥1 |
4.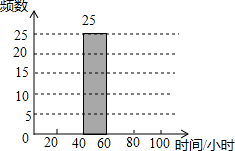 2015年12月18日天津日报报道,美国哈佛大学的学者们在进行了长达二十多年的跟踪研究之后,得出了一个惊人的结论:爱干家务的孩子与不爱干家务的孩子相比,失业率比例为1:15,犯罪率的比例为1:10.某校要求学生们寒假在家帮助父母做些力所能及的家务,李翰同学在开学初对本校部分学生寒假期间在家做家务的时间进行了抽样调查(时间取整小时),整理数据后绘制成频数分布表如图所示的频数分布直方图.
2015年12月18日天津日报报道,美国哈佛大学的学者们在进行了长达二十多年的跟踪研究之后,得出了一个惊人的结论:爱干家务的孩子与不爱干家务的孩子相比,失业率比例为1:15,犯罪率的比例为1:10.某校要求学生们寒假在家帮助父母做些力所能及的家务,李翰同学在开学初对本校部分学生寒假期间在家做家务的时间进行了抽样调查(时间取整小时),整理数据后绘制成频数分布表如图所示的频数分布直方图.
(1)将频数分布表和频数分布直方图补全;
(2)为了鼓励学生在家帮助父母做些力所能及的家务,要确定一个时间标准,若要使62%的学生达到这个标准,你觉得这个时间标准应定为多少?
 2015年12月18日天津日报报道,美国哈佛大学的学者们在进行了长达二十多年的跟踪研究之后,得出了一个惊人的结论:爱干家务的孩子与不爱干家务的孩子相比,失业率比例为1:15,犯罪率的比例为1:10.某校要求学生们寒假在家帮助父母做些力所能及的家务,李翰同学在开学初对本校部分学生寒假期间在家做家务的时间进行了抽样调查(时间取整小时),整理数据后绘制成频数分布表如图所示的频数分布直方图.
2015年12月18日天津日报报道,美国哈佛大学的学者们在进行了长达二十多年的跟踪研究之后,得出了一个惊人的结论:爱干家务的孩子与不爱干家务的孩子相比,失业率比例为1:15,犯罪率的比例为1:10.某校要求学生们寒假在家帮助父母做些力所能及的家务,李翰同学在开学初对本校部分学生寒假期间在家做家务的时间进行了抽样调查(时间取整小时),整理数据后绘制成频数分布表如图所示的频数分布直方图. | 时间段(小时) | 频数 | 频率 |
| 0-20 | ||
| 20-40 | 20 | 25% |
| 40-60 | 25 | |
| 60-80 | 15 | |
| 80-100 | 12.5% |
(2)为了鼓励学生在家帮助父母做些力所能及的家务,要确定一个时间标准,若要使62%的学生达到这个标准,你觉得这个时间标准应定为多少?
