题目内容
17.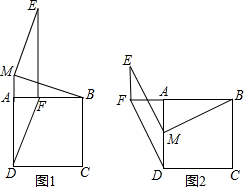 正方形ABCD的边长是5,点M是直线AD上一点,连接BM,将线段BM绕点M逆时针旋转90°得到线段ME,在直线AB上取点F,使AF=AM,且点F与点E在AD同侧,连接EF,DF.
正方形ABCD的边长是5,点M是直线AD上一点,连接BM,将线段BM绕点M逆时针旋转90°得到线段ME,在直线AB上取点F,使AF=AM,且点F与点E在AD同侧,连接EF,DF.(1)如图?1,当点M在DA延长线上时,求证:△ADF≌△ABM;
(2)如图2?,当点M在线段AD上时,四边形DFEM是否还是平行四边形,说明理由;
(3)在(2)的条件下,线段AM与线段AD有什么数量关系时,四边形DFEM的面积最大?并求出这个面积的最大值.
分析 (1)根据SAS即可证明;
(2)只要证明EM=DF,EM∥DF即可解决问题;
(3)如图2中,设DM=x,则AM=AF=5-x,构建二次函数,理由二次函数的性质即可解决问题;
解答 (1)证明:如图1中,
∵四边形ABCD是正方形,
∴∠DAF=∠BAM=90,AD=AB,
在△ADF和△ABM中,
$\left\{\begin{array}{l}{AF=AM}\\{∠DAF=∠BAM}\\{AD=AB}\end{array}\right.$,
∴△ADF≌△ABM.
(2)如图2中,结论:四边形DFEM是平行四边形.
理由:延长BM交DF于K.
∵△ADF≌△ABM,
∴DF=BM,∠ABM=∠ADF,
∵EM=BM,
∴EM=DF,
∵∠ABM+∠AMB=90°,∠AMB=∠DMK,
∴∠ADF+∠DMK=90°,
∴∠BKD=90°,
∵∠EMB=90°,
∴∠EMB=∠BKF=90°,
∴EM∥DF,
∴四边形EFDM是平行四边形.
(3)如图2中,设DM=x,则AM=AF=5-x,
S平行四边形EFDM=DM•AF=x(5-x)=-(x-$\frac{5}{2}$)2+$\frac{25}{4}$,
∵-1<0,
∴x=$\frac{5}{2}$时,平行四边形EFDM的面积最大,最大面积为$\frac{25}{4}$,
∴当AM=$\frac{1}{2}$AD时,平行四边形EFDM的面积最大,最大面积为$\frac{25}{4}$.
点评 本题考查四边形综合题、正方形的性质、全等三角形的判定和性质、二次函数的性质等知识,解题的关键是灵活运用所学知识解决问题,学会构建二次函数解决最值值问题,属于中考压轴题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 在△ABC中,∠A=160°.
在△ABC中,∠A=160°.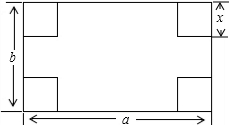 如图,小明想把一长为a,宽为b的长方形硬纸片做成一个无盖的长方体盒子,于是在长方形纸片的四个角各剪去一个边长为x的小正方形,用代数式表示纸片剩余部分的周长2a+2b+2x.
如图,小明想把一长为a,宽为b的长方形硬纸片做成一个无盖的长方体盒子,于是在长方形纸片的四个角各剪去一个边长为x的小正方形,用代数式表示纸片剩余部分的周长2a+2b+2x.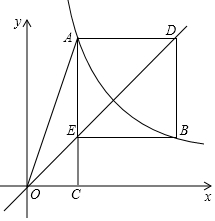 如图,在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过第一象限内的A,B两点,其中点A的坐标为(2,6),过点A作AC⊥x轴于点C,过点A作x轴的平行线,过点B作y轴的平行线,两线相交于点D,且AD=BD,直线OD交AC于点E,连接EB.
如图,在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过第一象限内的A,B两点,其中点A的坐标为(2,6),过点A作AC⊥x轴于点C,过点A作x轴的平行线,过点B作y轴的平行线,两线相交于点D,且AD=BD,直线OD交AC于点E,连接EB.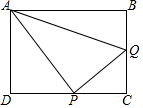 如图,已知矩形ABCD,AB=8cm,BC=6cm,点Q为BC中点,在DC上取一点P,使△APQ的面积等于18cm2,则DP的长度为4cm.
如图,已知矩形ABCD,AB=8cm,BC=6cm,点Q为BC中点,在DC上取一点P,使△APQ的面积等于18cm2,则DP的长度为4cm.
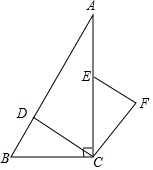 如图,在Rt△ABC中,∠ACB=90°,点D、E分别在AB、AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得到CF,连接EF.
如图,在Rt△ABC中,∠ACB=90°,点D、E分别在AB、AC上,CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得到CF,连接EF.