题目内容
6.已知二次三项式ax2+bx+c当x=2时,取得最小值-1;且它的两根的立方和为24,如果x=-1,那么这个二次三项式的值是12$\frac{1}{2}$.分析 根据二次三项式ax2+bx+c当x=2时,取得最小值-1;且它的两根的立方和为24,可以转化为一元二次函数的问题,从而可以求得a、b、c的值,进而可以求得当x=-1时的这个二次三项式的值,本题得以解决.
解答 解:由题意可得,
令y=ax2+bx+c,当x=2时,有最小值y=-1,设ax2+bx+c=0时的两个根为x1,x2,
则$\left\{\begin{array}{l}{-\frac{b}{2a}=2}\\{\frac{4ac-{b}^{2}}{4a}=-1}\\{{{x}_{1}}^{3}+{{x}_{2}}^{3}=({x}_{1}+{x}_{2})({{x}_{1}}^{2}-{x}_{1}{x}_{2}+{{x}_{2}}^{2})=24}\end{array}\right.$
又∵${x}_{1}+{x}_{2}=-\frac{b}{a}$,${{x}_{1}}^{2}-{x}_{1}{x}_{2}+{{x}_{2}}^{2}=({x}_{1}+{x}_{2})^{2}-3{x}_{1}{x}_{2}$,${x}_{1}{x}_{2}=\frac{c}{a}$,
解得,$\left\{\begin{array}{l}{a=\frac{3}{2}}\\{b=-6}\\{c=5}\end{array}\right.$
∴当x=-1时,y=a-b+c=$\frac{3}{2}-(-6)+5=\frac{3}{2}+6+5=12\frac{1}{2}$,
故答案为:12$\frac{1}{2}$.
点评 本题考查根与系数的关系,解题的关键是明确根与系数的关系,利用数学中转化的数学思想将所求问题转化为二次函数的问题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
16.不等式1≤$\frac{x-2}{3}$<5的解集是( )
| A. | 3≤x≤15 | B. | 5≤x<13 | C. | 5≤x<17 | D. | -3≤x<15 |
1.已知关于x的方程x2-kx-4=0的一个根为x=3,则实数k的值为( )
| A. | 5 | B. | 3 | C. | $\frac{3}{5}$ | D. | $\frac{5}{3}$ |
15.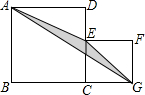 如图,正方形ABCD和EFGC中,左右两个正方形边长分别为a、b,用代数式表示阴影部分△AEG的面积为( )
如图,正方形ABCD和EFGC中,左右两个正方形边长分别为a、b,用代数式表示阴影部分△AEG的面积为( )
 如图,正方形ABCD和EFGC中,左右两个正方形边长分别为a、b,用代数式表示阴影部分△AEG的面积为( )
如图,正方形ABCD和EFGC中,左右两个正方形边长分别为a、b,用代数式表示阴影部分△AEG的面积为( )| A. | a2-b2 | B. | $\frac{2}{3}({a}^{2}-{b}^{2})$ | C. | $\frac{1}{2}{b}^{2}$ | D. | $\frac{1}{2}{a}^{2}$ |
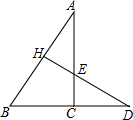 如图所示,DH⊥AB于H,AC⊥BD于C,DH与AC相交于点E,仔细观察图形,回答以下问题:
如图所示,DH⊥AB于H,AC⊥BD于C,DH与AC相交于点E,仔细观察图形,回答以下问题: 某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75,其图象如图所示.
某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75,其图象如图所示.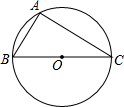 如图,已知BC为⊙O的直径,△ABC内接于⊙O,AB=2,∠C=30°.
如图,已知BC为⊙O的直径,△ABC内接于⊙O,AB=2,∠C=30°.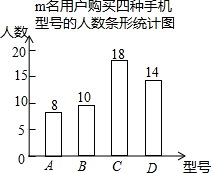 为了了解用户对某国手机的A、B、C、D四种型号的购买情况,某手机经销商随机对m名该手机用户的购买型号进行了调查,将调查数据整理并绘制成如图的统计图,根据统计图提供的信息,解答下列问题:
为了了解用户对某国手机的A、B、C、D四种型号的购买情况,某手机经销商随机对m名该手机用户的购买型号进行了调查,将调查数据整理并绘制成如图的统计图,根据统计图提供的信息,解答下列问题: