题目内容
4.如图(1),在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),将线段AB先向上平移2个单位长度,再向右平移1个单位长度,得到线段CD,连接AC,BD.(1)求点C,D的坐标及S四边形ABDC;
(2)点Q在y轴上,且S△QAB=S四边形ABDC,求出点Q的坐标;
(3)如图(2),点P是线段BD上任意一个点(不与B、D重合),连接PC、PO,试探索∠DCP、∠CPO、∠BOP之间的关系,并证明你的结论.

分析 (1)根据平移直接得到点C,D坐标,用面积公式计算;
(2)设出Q的坐标,OQ=|m|,用S△QAB=S四边形ABDC建立方程,解方程即可;
(3)作出辅助线,平行线,用两直线平行,内错角相等,即可.
解答 解:(1)∵线段AB先向上平移2个单位长度,再向右平移1个单位长度,得到线段CD,
且(-1,0),B(3,0),
∴C(0,2),D(4,2);
∵AB=4,OC=2,
∴S四边形ABDC=AB×OC=8;
(2)∵点Q在y轴上,设Q(0,m),
∴OQ=|m|,
∴S△QAB=$\frac{1}{2}$×AB×OQ=$\frac{1}{2}$×4×|m|=2|m|,
∵S四边形ABDC=8,
∴2|m|=8,
∴m=4或m=-4,
∴Q(0,4)或Q(0,-4).
(3)如图,
∵线段CD是线段AB平移得到,
∴CD∥AB,
作PE∥AB,
∴CD∥PE,
∴∠CPE=∠DCP,
∵PE∥AB,
∴∠OPE=∠BOP,
∴∠CPO=∠CPE+∠OPE=∠DCP+∠BOP,
∴∠CPO=∠DCP+∠BOP.
点评 此题是几何变换综合题,主要考查了平移得性质,计算三角形面积的方法,平行线的判定和性质,解本题的关键用面积建立方程或计算,作出辅助线是解本题的难点.

练习册系列答案
相关题目
15.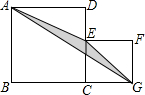 如图,正方形ABCD和EFGC中,左右两个正方形边长分别为a、b,用代数式表示阴影部分△AEG的面积为( )
如图,正方形ABCD和EFGC中,左右两个正方形边长分别为a、b,用代数式表示阴影部分△AEG的面积为( )
 如图,正方形ABCD和EFGC中,左右两个正方形边长分别为a、b,用代数式表示阴影部分△AEG的面积为( )
如图,正方形ABCD和EFGC中,左右两个正方形边长分别为a、b,用代数式表示阴影部分△AEG的面积为( )| A. | a2-b2 | B. | $\frac{2}{3}({a}^{2}-{b}^{2})$ | C. | $\frac{1}{2}{b}^{2}$ | D. | $\frac{1}{2}{a}^{2}$ |
19.若关于x的一元二次方程x2-(a+5)x+8a=0的两个实数根分别为2和b,则ab=( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
13.下列图形中既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75,其图象如图所示.
某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y=ax2+bx-75,其图象如图所示.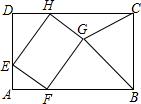 如图,矩形ABCD中,AD=6,CD=6+$2\sqrt{2}$,E为AD上一点,且AE=2,点F,H分别在边AB,CD上,四边形EFGH为矩形,点G在矩形ABCD的内部,则当△BGC为直角三角形时,AF的值是2或4.
如图,矩形ABCD中,AD=6,CD=6+$2\sqrt{2}$,E为AD上一点,且AE=2,点F,H分别在边AB,CD上,四边形EFGH为矩形,点G在矩形ABCD的内部,则当△BGC为直角三角形时,AF的值是2或4.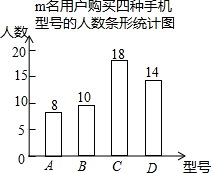 为了了解用户对某国手机的A、B、C、D四种型号的购买情况,某手机经销商随机对m名该手机用户的购买型号进行了调查,将调查数据整理并绘制成如图的统计图,根据统计图提供的信息,解答下列问题:
为了了解用户对某国手机的A、B、C、D四种型号的购买情况,某手机经销商随机对m名该手机用户的购买型号进行了调查,将调查数据整理并绘制成如图的统计图,根据统计图提供的信息,解答下列问题: