题目内容
8.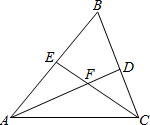 如图,在△ABC中,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.
如图,在△ABC中,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.(1)请你判断FE和FD之间的数量关系,并说明理由;
(2)求证:AE+CD=AC.
分析 (1)先证出∠CAF+∠ACF=60°,得出∠DFE=∠AFC=120°,证出∠ABC+∠DFE=180°,证出B、E、F、D四点共圆,得出$\widehat{FE}=\widehat{FD}$,即可得出FE=FD;
(2)在AC上截取AG=AE,连接GF,先证明△AGF≌△AEF,得出FG=FE,∠AFG=∠AFE=60°,再证明△CFG≌△CFD,得出CG=CD,即可得出结论.
解答 (1)解:FE=FD;理由如下:连接BF,如图所示: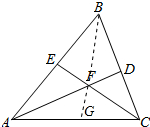 ∵∠ABC=60°,∠ABC+∠BAC+∠BCA=180°,
∵∠ABC=60°,∠ABC+∠BAC+∠BCA=180°,
∴∠BAC+∠BCA=120°,
∵AD、CE分别是∠BAC、∠BCA的平分线,
∴∠CAF=$\frac{1}{2}$∠BAC,∠ACF=$\frac{1}{2}$∠BCA,BF平分∠ABC,
∴∠CAF+∠ACF=$\frac{1}{2}$(∠BAC+∠BCA)=60°,∠ABF=∠CBF,
∴∠DFE=∠AFC=120°,∠DFC=∠AFE=60°,
∴∠ABC+∠DFE=180°,
∴B、E、F、D四点共圆,
∴$\widehat{FE}=\widehat{FD}$,
∴FE=FD;
(2)证明:在AC上截取AG=AE,连接GF,如图所示:
在△AGF和△AEF中,
$\left\{\begin{array}{l}{AG=AE}&{\;}\\{∠GAF=∠EAF}&{\;}\\{AF=AF}&{\;}\end{array}\right.$,
∴△AGF≌△AEF(SAS),
∴FG=FE,∠AFG=∠AFE=60°,
∴FG=FD,∠GFC=120°-60°=60°,
在△CFG和△CFD中,
$\left\{\begin{array}{l}{FG=∠FD}&{\;}\\{∠GFC=∠DFC=60°}&{\;}\\{FC=FC}&{\;}\end{array}\right.$,
∴△CFG≌△CFD(SAS),
∴CG=CD,
∴AE+CD=AG+CG=AC.
点评 本题考查了全等三角形的判定与性质、四点共圆、角平分线的定义、三角形内角和定理、圆周角定理;本题有一定难度,需要通过作辅助线证明四点共圆和三角形全等才能得出结论.

| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 有一个实数根 | D. | 没有实数根 |
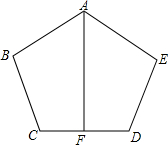 如图所示,已知AB=AE,∠ABC=∠AED,BC=ED,F是CD的中点,AF与CD有什么位置关系?说明理由.
如图所示,已知AB=AE,∠ABC=∠AED,BC=ED,F是CD的中点,AF与CD有什么位置关系?说明理由.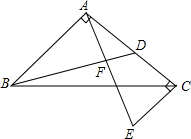 如图,在等腰直角三角形中,∠BAC=90°,AB=AC,点D是AC上一点,过点A作AF⊥BD,过点C作CE⊥AC的延长线于E,说明AE=BD.
如图,在等腰直角三角形中,∠BAC=90°,AB=AC,点D是AC上一点,过点A作AF⊥BD,过点C作CE⊥AC的延长线于E,说明AE=BD.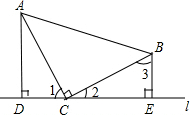 如图,在△ABC中,∠ACB=90°,CA=BC,直线l在△ABC的外部且过点C,AD⊥l,BE⊥l,垂足分别为点D、E.
如图,在△ABC中,∠ACB=90°,CA=BC,直线l在△ABC的外部且过点C,AD⊥l,BE⊥l,垂足分别为点D、E.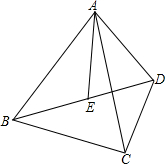 如图,AB=AC,AD=AE,∠BAC=∠DAE,BE与CD相等吗?为什么?
如图,AB=AC,AD=AE,∠BAC=∠DAE,BE与CD相等吗?为什么?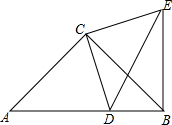 如图,AC=BC,∠CAB=∠CBA=45°,D为AB边上一个动点,CE=CD,∠CDE=∠CED=45°.
如图,AC=BC,∠CAB=∠CBA=45°,D为AB边上一个动点,CE=CD,∠CDE=∠CED=45°.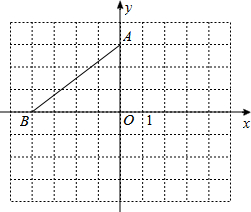 在平面直角坐标系中,点A的坐标是(0,3),点B在x轴上,将△AOB绕点A逆时针旋转90°得到△AEF,点O、B的对应点分别是点E、F.
在平面直角坐标系中,点A的坐标是(0,3),点B在x轴上,将△AOB绕点A逆时针旋转90°得到△AEF,点O、B的对应点分别是点E、F.