题目内容
5.解不等式组$\left\{\begin{array}{l}{x+1>\frac{3x-1}{2}}\\{2x-(x-3)≥5}\end{array}\right.$.分析 分别求出各不等式的解集,再求出其公共解集即可.
解答 解:$\left\{\begin{array}{l}x+1>\frac{3x-1}{2}①\\ 2x-(x-3)≥5②\end{array}\right.$,由①得,x<3,由②得,x≥2,
故不等式组的解集为:2≤x<3.
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
16.某车间有22名工人,每人每天可以生产1200个螺钉或2000个螺母,1个螺钉需要配2个螺母,为节约成本车间规定每天生产的螺钉和螺母刚好配套,设每天安排x个工人生产螺钉,则下列方程中符合题意的是( )
| A. | 2000(22-x)=2×1200x | B. | 2×2000(22-x)=1200x | ||
| C. | 1200(22-x)=2×2000x | D. | 2×1200(22-x)=2000x |
20.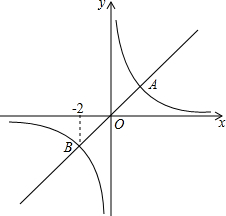 正比例函数y1=k1x的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A,B两点,其中点B的横坐标为-2,当y1<y2时,x的取值范围是( )
正比例函数y1=k1x的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A,B两点,其中点B的横坐标为-2,当y1<y2时,x的取值范围是( )
 正比例函数y1=k1x的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A,B两点,其中点B的横坐标为-2,当y1<y2时,x的取值范围是( )
正比例函数y1=k1x的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A,B两点,其中点B的横坐标为-2,当y1<y2时,x的取值范围是( )| A. | x<-2或x>2 | B. | x<-2或0<x<2 | C. | -2<x<0或0<x<2 | D. | -2<x<0或x>2 |
10.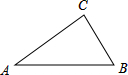 如图,△ABC中,∠C=90°,∠A=30°,AB=12,则BC=( )
如图,△ABC中,∠C=90°,∠A=30°,AB=12,则BC=( )
 如图,△ABC中,∠C=90°,∠A=30°,AB=12,则BC=( )
如图,△ABC中,∠C=90°,∠A=30°,AB=12,则BC=( )| A. | 6 | B. | 6$\sqrt{2}$ | C. | 6$\sqrt{3}$ | D. | 12 |
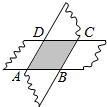 如图,用两张等宽的纸条交叉叠放在一起,重叠部分为四边形ABCD,它是一个特殊的四边形.
如图,用两张等宽的纸条交叉叠放在一起,重叠部分为四边形ABCD,它是一个特殊的四边形.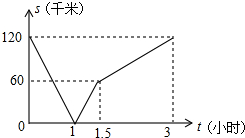 甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:干米),甲行驶的时间为s(单位:小时),s与t之间的函数关系如图所示,有下列结论:(汽车速度大于摩托车速度).①出发1小时,甲、乙在途中相遇;②出发1.5小时,甲行驶了60千米;③出发2小时,甲、乙相距8O干米;④出发3小时,甲、乙同时到达目的地;其中,正确结论的个数是( )
甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:干米),甲行驶的时间为s(单位:小时),s与t之间的函数关系如图所示,有下列结论:(汽车速度大于摩托车速度).①出发1小时,甲、乙在途中相遇;②出发1.5小时,甲行驶了60千米;③出发2小时,甲、乙相距8O干米;④出发3小时,甲、乙同时到达目的地;其中,正确结论的个数是( )