题目内容
13.(1)计算:2sin60°-(π-2016)0+(-$\frac{1}{2}$)-2+|2-$\sqrt{3}$|;(2)用配方法解一元二次方程:2x2+8x-1=0.
分析 (1)先计算三角函数、零指数幂、负整指数幂、去绝对值符号,再计算乘法,最后计算加减可得;
(2)常数项移到右边,方程二次项系数化为1,两边加上一次项系数一半的平方,变形后开方即可求出解.
解答 解:(1)原式=2×$\frac{\sqrt{3}}{2}$-1+4+2-$\sqrt{3}$
=$\sqrt{3}$-1+4+2-$\sqrt{3}$
=5;
(2)由2x2+8x-1=0得:2x2+8x=1,
x2+4x=$\frac{1}{2}$,
x2+4x+4=$\frac{1}{2}$+4,
(x+2)2=$\frac{9}{2}$,
x+2=±$\frac{3\sqrt{2}}{2}$,即x=-2±$\frac{3\sqrt{2}}{2}$
∴x1=$\frac{-4-3\sqrt{2}}{2}$,x2=$\frac{-4+3\sqrt{2}}{2}$.
点评 本题考查了实数的混合运算与配方法解一元二次方程,熟练掌握各自的解法是解本题的关键.

练习册系列答案
相关题目
1.分式$\frac{x-2}{x-3}$的值为0时,x的值是( )
| A. | x=0 | B. | x=2 | C. | x=3 | D. | x=2或x=3 |
8.若数据8,x,10,10,10的众数与平均数相同,则x的值为( )
| A. | 12 | B. | 10 | C. | 8 | D. | 2 |
1.下列方程中,解是x=2的是( )
| A. | 3x+1=2x-1 | B. | 3x-1=2x+1 | C. | 3x+2x-2=0 | D. | 3x+2x+2=0 |
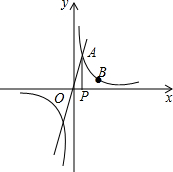 已知正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象交于点A,过点A作x轴的垂线,垂足为点P,已知△OAP的面积为1.
已知正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象交于点A,过点A作x轴的垂线,垂足为点P,已知△OAP的面积为1.
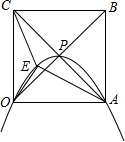 正方形OABC的边长为4,对角线相交于点P,抛物线L经过O、P、A三点,点E是正方形内的抛物线上的动点.
正方形OABC的边长为4,对角线相交于点P,抛物线L经过O、P、A三点,点E是正方形内的抛物线上的动点.