题目内容
10.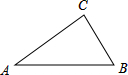 如图,△ABC中,∠C=90°,∠A=30°,AB=12,则BC=( )
如图,△ABC中,∠C=90°,∠A=30°,AB=12,则BC=( )| A. | 6 | B. | 6$\sqrt{2}$ | C. | 6$\sqrt{3}$ | D. | 12 |
分析 根据30°所对的直角边等于斜边的一半求解.
解答 解:∵∠C=90°,∠A=30°,AB=12,
∴BC=$\frac{1}{2}$AB=12×$\frac{1}{2}$=6,
故答选A.
点评 本题考查解直角三角形,解题的关键是正确的利用合适的边角关系.

练习册系列答案
相关题目
1.分式$\frac{x-2}{x-3}$的值为0时,x的值是( )
| A. | x=0 | B. | x=2 | C. | x=3 | D. | x=2或x=3 |
17.某市为了方便广大群众绿色出行,在城市设置了若干个站点,进行公共自行车租赁服务,并实行累加计费,具体计费标准如下:
(例如:使用者用车5小时,则系统收费:0+1+2+3+3=9元)
(1)九年级同学集体出游,若租赁自行车的时间是7个小时(每人一辆),其他花费是300元,请写出这次出游的总费用y(元)和学生人数x(名)之间的关系式;
(2)由于一名同学临时有事,仅仅租了两个小时就归还了自行车,这次出游的总费用是886元,请问共有多少名同学(包括这名有事的同学在内)参加了这次出游?
| 租赁时间<1小时 | 免费 |
| 1小时<租赁时间≤2小时 | 1元 |
| 2小时<租赁时间≤3小时 | 2元 |
| 租赁时间>3小时 | 3元/小时(不足1小时按1小时计) |
| 租赁时间≤24小时 | 最高收费30元 |
(1)九年级同学集体出游,若租赁自行车的时间是7个小时(每人一辆),其他花费是300元,请写出这次出游的总费用y(元)和学生人数x(名)之间的关系式;
(2)由于一名同学临时有事,仅仅租了两个小时就归还了自行车,这次出游的总费用是886元,请问共有多少名同学(包括这名有事的同学在内)参加了这次出游?
18.某工厂计划在规定时间内生产2400个零件,若每天比原计划多生产3个零件,则在规定时间内可以多生产30个零件,求原计划每天生产的零件个数.设原计划每天生产的零件个数为x个,由题意得( )
| A. | $\frac{2400}{x}$=$\frac{2400+30}{x+3}$ | B. | $\frac{2400+30}{x}$=$\frac{2400}{x-3}$ | ||
| C. | $\frac{2400-30}{x-3}$=$\frac{2400}{x}$ | D. | $\frac{2400-30}{x}$=$\frac{2400}{x-3}$ |
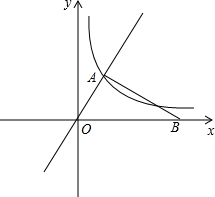 如图,在平面直角坐标系xOy中,已知直线y=$\sqrt{3}$x与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点A,且点A的横坐标为1,点B是x轴正半轴上一点,且AB⊥OA.
如图,在平面直角坐标系xOy中,已知直线y=$\sqrt{3}$x与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点A,且点A的横坐标为1,点B是x轴正半轴上一点,且AB⊥OA.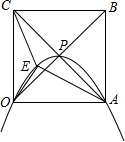 正方形OABC的边长为4,对角线相交于点P,抛物线L经过O、P、A三点,点E是正方形内的抛物线上的动点.
正方形OABC的边长为4,对角线相交于点P,抛物线L经过O、P、A三点,点E是正方形内的抛物线上的动点.