题目内容
9.已知点A(-1,-1)在抛物线y=(k2-1)x2-2(k-2)x+1上,点B与点A关于抛物线的对称轴对称,求k的值和点B的坐标.分析 将A点坐标代入抛物线的解析式中,即可求得k的值;从而确定抛物线的解析式和对称轴方程,根据A、B关于抛物线的对称轴对称,即可得到点B的坐标;
解答 解:根据题意,将x=-1,y=-1,代入抛物线的解析式,得
(k2-1)×(-1)2-2(k-2)×(-1)+1=-1
解得k1=1,k2=-3.
由于k2-1≠0,所以k=-3.
抛物线的解析式是y=8x2+10x+1,
对称轴为直线x=-$\frac{b}{2a}$=-$\frac{10}{2×8}$=-$\frac{5}{8}$,
∵点B和点A(-1,-1)关于直线x=-$\frac{5}{8}$对称,
∴B(-$\frac{1}{4}$,0).
点评 此题主要考查了二次函数图象上点的坐标特征,图象上点的坐标适合解析式是解题的关键.

练习册系列答案
相关题目
20.若x>y,则下列式子中错误的是( )
| A. | x-3>y-3 | B. | x+3>y+3 | C. | $\frac{1}{3}x>\frac{1}{3}y$ | D. | -3x>-3y |
17.要使(x+m)(x-3)的结果中不含x的一次项,则m等于( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
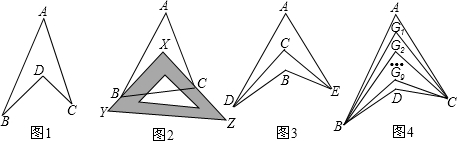
 如图,已知AB=AC,BD=BC,AD=DE=EB,试求∠A的度数.
如图,已知AB=AC,BD=BC,AD=DE=EB,试求∠A的度数. 如图所示,在△ABC中,∠A=2∠B=60°,CD⊥AB于点D,点M是AB的中点,求证:2DM=AC.
如图所示,在△ABC中,∠A=2∠B=60°,CD⊥AB于点D,点M是AB的中点,求证:2DM=AC.