题目内容
14.平面上有n个点,任意三点不在同一直线上,共可确定m条直线,则m,n之间的关系式为m=$\frac{1}{2}$n2$-\frac{1}{2}n$.分析 2个点可确定1条直线,3个点可确定3=1+2条直线,4个点可确定6=1+2+3条直线,所以n个点可确定1+2+3+4+…(n-1)=$\frac{1+n-1}{2}×(n-1)$=$\frac{1}{2}n$(n-1)=m.
解答 解:∵2个点可确定1条直线,3个点可确定3=1+2条直线,4个点可确定6=1+2+3条直线,
∴n个点可确定1+2+3+4+…(n-1)=$\frac{1+n-1}{2}×(n-1)$=$\frac{1}{2}n$(n-1)条直线,
∴m=$\frac{1}{2}$n2-$\frac{1}{2}n$.
故答案为:m=$\frac{1}{2}$n2-$\frac{1}{2}n$.
点评 本题主要考查了两点确定一条直线,根据两点确定一条直线,发现规律是解答此题的关键.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
2.北京时间2011年3月11日13时46分,日本发生9.0级特大地震,某日资公司为筹集善款,对其日本原产品进行大幅度销售,有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
(1)设分配给甲店A型产品x件,这家公司卖出这100件产品的总利润为W(元),求W关于x的函数关系式,并求出x的取值范围;
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来;
(3)为了促销,公司决定仅对甲店A型产品让利销售,每件让利a元,但让利后A型产品的每件利润仍高于甲店B型产品的每件利润.甲店的B型产品以及乙店的A、B型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
| A型利润 | B型利润 | |
| 甲店 | 200 | 170 |
| 乙店 | 160 | 150 |
(2)若公司要求总利润不低于17560元,说明有多少种不同分配方案,并将各种方案设计出来;
(3)为了促销,公司决定仅对甲店A型产品让利销售,每件让利a元,但让利后A型产品的每件利润仍高于甲店B型产品的每件利润.甲店的B型产品以及乙店的A、B型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
 如图,已知AB为⊙O的直径,CE切⊙O于C点,过B点的直线BD交直线CE于D点,如果BC平分∠ABD.求证:BD⊥CE.
如图,已知AB为⊙O的直径,CE切⊙O于C点,过B点的直线BD交直线CE于D点,如果BC平分∠ABD.求证:BD⊥CE.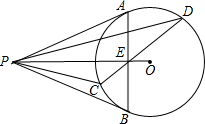 如图,已知P为⊙O外一点,PA切⊙O于点A,PB切⊙O于点B,AB交OP于点E,弦CD过E点.求证:∠APC=∠BPD.
如图,已知P为⊙O外一点,PA切⊙O于点A,PB切⊙O于点B,AB交OP于点E,弦CD过E点.求证:∠APC=∠BPD. 如图,?ABCD的边BC长为6,中点为原点,AB长为2,∠ABC=60°,求它的四个顶点的坐标.
如图,?ABCD的边BC长为6,中点为原点,AB长为2,∠ABC=60°,求它的四个顶点的坐标.