题目内容
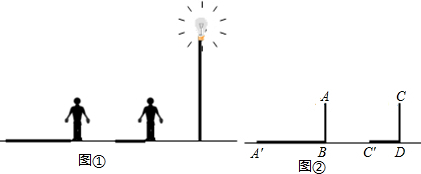
 如图所示,∠DAB=60°,CD⊥AD,CB⊥AB,且AB=2,CD=1,求AD和BC的长.
如图所示,∠DAB=60°,CD⊥AD,CB⊥AB,且AB=2,CD=1,求AD和BC的长.考点:勾股定理,含30度角的直角三角形
专题:
分析:延长AB,DC相交于点E,根据直角三角形的性质求出∠E的度数,设BC=x,则CE=2x,BE=
x,同理,在Rt△ADE中,AD=
AB=
(2+
x),DE=CD+CE=1+2x,再根据勾股定理求出x的值即可.
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
解答: 解:延长AB,DC相交于点E,
解:延长AB,DC相交于点E,
∵∠DAB=60°,CD⊥AD,CB⊥AB,
∴∠E=30°.
设BC=x,则CE=2x,BE=
x,
同理,在Rt△ADE中,AD=
AE=
(2+
x),DE=CD+CE=1+2x=AE•
,即1+2x=(2+
x)•
,
∴x=
-1,
∴AD=
AE=
[1+
(
-1)]=2-
;
BC=
-1.
 解:延长AB,DC相交于点E,
解:延长AB,DC相交于点E,∵∠DAB=60°,CD⊥AD,CB⊥AB,
∴∠E=30°.
设BC=x,则CE=2x,BE=
| 3 |
同理,在Rt△ADE中,AD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 3 |
| ||
| 2 |
∴x=
| 3 |
∴AD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 2 |
BC=
| 3 |
点评:本题考查的是勾股定理,根据题意构造出直角三角形,利用直角三角形的性质求解是解答此题的关键.

练习册系列答案
相关题目
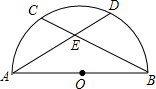 如图,已知:AB是⊙O的直径,C、D是弧
如图,已知:AB是⊙O的直径,C、D是弧 |
| AB |
| A、150° | B、135° |
| C、140° | D、120° |
函数表达式y=
中的自变量x取值范围是( )
| 1 | ||
|
| A、x≥2 | B、x≤2 |
| C、x>2 | D、x<2 |
 如图,△ABC中,AD是∠BAC的平分线,AD的垂直平分线AD交于点E,交BC的延长线于点F.试说明:△ABF∽△CAF.
如图,△ABC中,AD是∠BAC的平分线,AD的垂直平分线AD交于点E,交BC的延长线于点F.试说明:△ABF∽△CAF. 如图,小明在河岸的A处观察对岸C处的一棵树,视线与河岸30°角;同时,小亮在距小明100米的河岸B观察对岸D处的一棵树,视线与河岸成75°角.已知河宽90米,且两岸平行,求河对岸C、D两棵树的距离.(参考数据:
如图,小明在河岸的A处观察对岸C处的一棵树,视线与河岸30°角;同时,小亮在距小明100米的河岸B观察对岸D处的一棵树,视线与河岸成75°角.已知河宽90米,且两岸平行,求河对岸C、D两棵树的距离.(参考数据: 已知:如图△ABC中,BD和CE是三角形的高,M为BC的中点,P为DE的中点.求证:PM⊥DE.
已知:如图△ABC中,BD和CE是三角形的高,M为BC的中点,P为DE的中点.求证:PM⊥DE. 如图,已知AD∥BC,∠BAD=∠BCD,AE平分∠BAD,CF平分∠BCD,求证:AE∥FC.
如图,已知AD∥BC,∠BAD=∠BCD,AE平分∠BAD,CF平分∠BCD,求证:AE∥FC.