题目内容
 如图,小明在河岸的A处观察对岸C处的一棵树,视线与河岸30°角;同时,小亮在距小明100米的河岸B观察对岸D处的一棵树,视线与河岸成75°角.已知河宽90米,且两岸平行,求河对岸C、D两棵树的距离.(参考数据:
如图,小明在河岸的A处观察对岸C处的一棵树,视线与河岸30°角;同时,小亮在距小明100米的河岸B观察对岸D处的一棵树,视线与河岸成75°角.已知河宽90米,且两岸平行,求河对岸C、D两棵树的距离.(参考数据:| 3 |
| 2 |
考点:解直角三角形的应用
专题:
分析:如图,过点A作BD的平行线交直线CD于F,构建平行四边形ABDF,则FD=AB=100,作AE⊥CD于E,作FH⊥AC于H,构建直角三角形,通过解直角三角形来求CD的距离.
解答: 解:如图,过点A作BD的平行线交直线CD于F,则FD=AB=100,
解:如图,过点A作BD的平行线交直线CD于F,则FD=AB=100,
作AE⊥CD于E,作FH⊥AC于H,则∠AFE=∠BDE=75°,
∴∠EAF=15°.
∵∠EAC=90°-30°=60°,
∴∠EAC=60°-15°=45°,
设AH=FH=x.
在Rt△EAC中,AE=90°,∠C=30°,∴AC=2AE=180.
在Rt△CFH中,FC=
x,∴x+
x=180,
解得:x=90(
-1),
FC=2x=180(
-1),CD=FC-FD=180(
-1)-100=26(米).
 解:如图,过点A作BD的平行线交直线CD于F,则FD=AB=100,
解:如图,过点A作BD的平行线交直线CD于F,则FD=AB=100,作AE⊥CD于E,作FH⊥AC于H,则∠AFE=∠BDE=75°,
∴∠EAF=15°.
∵∠EAC=90°-30°=60°,
∴∠EAC=60°-15°=45°,
设AH=FH=x.
在Rt△EAC中,AE=90°,∠C=30°,∴AC=2AE=180.
在Rt△CFH中,FC=
| 3 |
| 3 |
解得:x=90(
| 3 |
FC=2x=180(
| 3 |
| 3 |
点评:本题考查了解直角三角形.关键把实际问题转化为数学问题加以计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,正方形A,B,C,D的顶点ABCD都在坐标轴上,已知OA=OB=OC=OD=
如图,正方形A,B,C,D的顶点ABCD都在坐标轴上,已知OA=OB=OC=OD=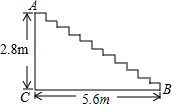 如图,某商场重新装修后,准备在大厅的主楼梯上铺设一种红色的地毯,已知这种地毯的价格为40元/m2,主楼梯的宽为3m,其侧面如图所示,则铺设这段楼梯至少需要多少元?
如图,某商场重新装修后,准备在大厅的主楼梯上铺设一种红色的地毯,已知这种地毯的价格为40元/m2,主楼梯的宽为3m,其侧面如图所示,则铺设这段楼梯至少需要多少元? (1)如图,已知∠B+∠D=∠BED,求证:AB∥CD,
(1)如图,已知∠B+∠D=∠BED,求证:AB∥CD, 如图,AB∥CD,∠B=60°,∠O=40°,则∠D=
如图,AB∥CD,∠B=60°,∠O=40°,则∠D= 如图,二次函数的图象经过A(1,0),B(3,0)及在正比例函数y=x上的动点P
如图,二次函数的图象经过A(1,0),B(3,0)及在正比例函数y=x上的动点P 如图,如果AC⊥BC,CD⊥AB,∠1=∠2,那么下列结论中正确的个数是( )
如图,如果AC⊥BC,CD⊥AB,∠1=∠2,那么下列结论中正确的个数是( ) 如图所示,∠DAB=60°,CD⊥AD,CB⊥AB,且AB=2,CD=1,求AD和BC的长.
如图所示,∠DAB=60°,CD⊥AD,CB⊥AB,且AB=2,CD=1,求AD和BC的长.