Question

6．已知圆O的内接六边形周长为12cm，则圆O的面积是4πcm²（结果保留π）．

Answer 1

分析 首先求出∠AOB=$\frac{1}{6}$×360°，进而证明△OAB为等边三角形，得出OA=AB=2cm，问题即可解决．

解答 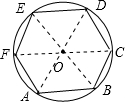解：如图，
∵⊙O的内接正六边形ABCDEF的周长为12cm，
∴边长AB=2cm，
∵∠AOB=$\frac{1}{6}$×360°=60°，且OA=OB，
∴△OAB为等边三角形，
∴OA=AB=2，
即该圆的半径为2，
∴圆O的面积=2²π=4π；
故答案为：4π．

点评 本题考查了正多边形和圆、正六边形的性质、等边三角形的判定与性质、圆的面积公式；熟练掌握正六边形的性质，求出圆的半径是解决问题的关键．