题目内容
3.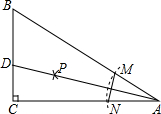 如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法错误的是( )
如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法错误的是( )| A. | ∠BAD=∠CAD | |
| B. | 点D到AB边的距离就等于线段CD的长 | |
| C. | S△ABD=S△ACD | |
| D. | AD垂直平分MN |
分析 根据作图方法可得AD平分∠CAB,由角平分线的定义和性质可得A、B说法正确,根据三角形的面积公式可得C错误,根据题目所给条件可证明△AMO≌△ANO,进而可得MO=NO,∠MOA=∠NOA,从而证得D选项说法正确.
解答 解:根据题意可得AD平分∠CAB,
∵AD平分∠CAB,
∴∠BAD=∠CAD,故A说法正确;
∵AD平分∠CAB,
∴点D到AB边的距离就等于线段CD的长,故B说法正确;
∵点D到AB边的距离就等于线段CD的长,AB>AC,
∴S△ABD>S△ACD,故C说法错误;
在△AMO和△ANO中,
$\left\{\begin{array}{l}{AM=AN}\\{∠MAO=∠NAO}\\{AO=AO}\end{array}\right.$,
∴△AMO≌△ANO(SAS),
∴MO=NO,∠MOA=∠NOA,
∵∠MOA+∠NOA=180°,
∴∠MOA=90°,
∴AO⊥MN,
∴AD垂直平分MN,故D说法正确.
故选:C.
点评 此题主要考查了基本作图,关键是掌握角平分线的作法.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
14.下列二次根式中是最简二次根式的个数有( )
$\sqrt{0.5}$,$\sqrt{5}$,$\sqrt{50}$,$\sqrt{{a}^{2}b}$(b>0),$\sqrt{25}$.
$\sqrt{0.5}$,$\sqrt{5}$,$\sqrt{50}$,$\sqrt{{a}^{2}b}$(b>0),$\sqrt{25}$.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
18.下列所示的图案中,有且仅有一条对称轴的是( )
| A. |  | B. |  | C. |  | D. |  |
15.方程2x2-$\sqrt{5}$x-3=0的两根是( )
| A. | x=$\frac{\sqrt{5}±\sqrt{11}}{2}$ | B. | x=$\frac{\sqrt{5}±\sqrt{29}}{4}$ | C. | x=$\frac{-\sqrt{5}±\sqrt{29}}{2}$ | D. | x=$\frac{-\sqrt{5}±\sqrt{29}}{4}$ |
 小明和小亮用下面两个转盘做“配紫色”游戏.分别转动两个转盘,若配成紫色,则小明赢,否则小亮赢.这个游戏对双方公平吗?说明理由.怎样将此游戏规则修改一下,使游戏双方都公平呢?
小明和小亮用下面两个转盘做“配紫色”游戏.分别转动两个转盘,若配成紫色,则小明赢,否则小亮赢.这个游戏对双方公平吗?说明理由.怎样将此游戏规则修改一下,使游戏双方都公平呢?