题目内容
13.(1)计算:$\sqrt{24}+\sqrt{48}÷\sqrt{3}-2\sqrt{\frac{1}{2}}×\sqrt{12}$(2)解方程:2x2-5x-3=0.
分析 (1)先根据二次根式的乘除法则运算,然后合并即可;
(2)利用因式分解法解方程.
解答 解:(1)原式=2$\sqrt{6}$+$\sqrt{48÷3}$-2$\sqrt{\frac{1}{2}×12}$
=2$\sqrt{6}$+4-2$\sqrt{6}$
=4;
(2)(2x-3)(x+1)=0,
2x-3=0或x+1=0,
所以x1=$\frac{3}{2}$,x2=-1.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了因式分解法解一元二次方程.

练习册系列答案
相关题目
3.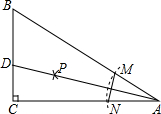 如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法错误的是( )
如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法错误的是( )
 如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法错误的是( )
如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法错误的是( )| A. | ∠BAD=∠CAD | |
| B. | 点D到AB边的距离就等于线段CD的长 | |
| C. | S△ABD=S△ACD | |
| D. | AD垂直平分MN |
3.下列命题不是真命题的是( )
| A. | 等腰梯形对角线相等 | |
| B. | 一组对边平行另一组对边相等的四边形是平行四边形 | |
| C. | 矩形的对角线相等 | |
| D. | 对角线互相垂直且相等的四边形是正方形 |