题目内容
18.根据不等式的基本性质,把下列不等式化为“x>a”或“x<a“的形式:(1)x+3>3x-5
(2)$\frac{1}{2}$x<$\frac{1}{2}$(6-x)
(3)-3x+2<2x+3.
分析 (1)两边同加-3x-3,再同除以-2,改变不等号的方向.
(2)两边同乘2,不改变不等号的方向,再边同加x,再同除以2,不改变不等号的方向;
(4)两边同加-2x-2,再同除以-5,改变不等号的方向.
解答 解:(1)x+3>3x-5
x+3-3x-3>3x-5-3x-3
-2x>-8
x<4;
(2)$\frac{1}{2}$x<$\frac{1}{2}$(6-x)
x<6-x
x+x<6-x+x
2x<6
x<3;
(3)-3x+2<2x+3
-3x+2-2x-2<2x+3-2x-2
-5x<1,
x>-$\frac{1}{5}$.
点评 主要考查了不等式的基本性质:(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变;(2)不等式两边乘(或除以)同一个正数,不等号的方向不变;(3)不等式两边乘(或除以)同一个负数,不等号的方向改变.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.下列说法中,正确的是( )
| A. | 平方是本身的数是0 | B. | 立方是本身的数是0、1 | ||
| C. | 绝对值是本身的数是正数 | D. | 倒数是本身的数是±1 |
13.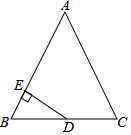 如图.在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB,垂足为点E,则DE等于( )
如图.在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB,垂足为点E,则DE等于( )
 如图.在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB,垂足为点E,则DE等于( )
如图.在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB,垂足为点E,则DE等于( )| A. | $\frac{10}{13}$ | B. | $\frac{15}{13}$ | C. | $\frac{45}{13}$ | D. | $\frac{60}{13}$ |
3.关于x的方程3x2-5=2x的二次项系数和一次项系数分别是( )
| A. | 3,-2 | B. | 3,2 | C. | 3,5 | D. | 5,2 |
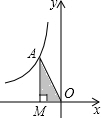 如图(图象在第二象限),若点A在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,AM⊥x轴于点M,△AMO的面积为5,则k=-10.
如图(图象在第二象限),若点A在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,AM⊥x轴于点M,△AMO的面积为5,则k=-10. 已知:数a,b,c 在数轴上的对应点如图所示,化简|a+b|-|-3c|-|c-a|的值是b+4c.
已知:数a,b,c 在数轴上的对应点如图所示,化简|a+b|-|-3c|-|c-a|的值是b+4c. 如图△ABC是等边三角形,BD平分∠ABC,延长BC至E,连结DE,此时DB=DE.求证:CE=CD.
如图△ABC是等边三角形,BD平分∠ABC,延长BC至E,连结DE,此时DB=DE.求证:CE=CD.