Question

7．如图，在平面直角坐标系中，过格点A、B、C作一圆弧．
（1）直接写出该圆弧所在圆的圆心D的坐标； 
（2）求弧AC的长（结果保留π）；
（3）连接AC、BC，则sinC=$\frac{\sqrt{5}}{5}$．

Answer 1

分析 （1）根据垂径定理的推论：弦的垂直平分线必过圆心，可以作弦AB和BC的垂直平分线，交点即为圆心，写出圆心坐标即可；
（2）根据正方形的性质和勾股定理以及弧长公式计算即可；
（3）根据正弦的定义计算即可．

解答 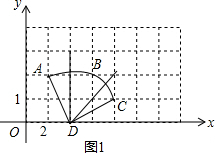解：（1）根据垂径定理的推论：弦的垂直平分线必过圆心，
作弦AB和BC的垂直平分线，交点D即为圆心．
如图1所示，则圆心D的坐标是（2，0）；
（2）由图1可知，∠ADC=90°，AD=$\sqrt{5}$，
∴弧AC的长为：$\frac{90π×\sqrt{5}}{180}$=$\frac{\sqrt{5}}{2}$π；
（3）如图2，由勾股定理得AE=$\sqrt{2}$，AC=$\sqrt{10}$，
由正方形的性质和格点的性质可知，∠AEC=90°，
则sinC=$\frac{AE}{AC}$=$\frac{\sqrt{2}}{\sqrt{10}}$=$\frac{\sqrt{5}}{5}$，
故答案为：$\frac{\sqrt{5}}{5}$．

点评 本题考查的是垂径定理、勾股定理、弧长的计算，掌握弦的垂直平分线经过圆心、弧长的计算公式是解题的关键．