题目内容
2. 如图,⊙O的半径为2,过点A(4,0)的直线与⊙O相切于点B,则点B的坐标为(1,$\sqrt{3}$).
如图,⊙O的半径为2,过点A(4,0)的直线与⊙O相切于点B,则点B的坐标为(1,$\sqrt{3}$).
分析 连接OB,根据切线的性质得出OB⊥AB,作BD⊥OA于D,易证得△BOD∽△AOB,得到$\frac{OD}{OB}$=$\frac{OB}{OA}$,求得OD的长,根据勾股定理即可求出BD的长,从而求得B点的坐标.
解答 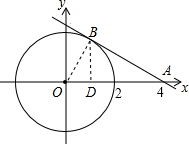 解:如图,连接OB;
解:如图,连接OB;
∵直线AB与⊙O相切于点B,
∴OB⊥AB,
∵⊙O的半径为2,点A(4,0),
∴OB=2,OA=4,
作BD⊥OA于D,
∵∠BDO=∠ABO=90°,∠BOD=∠AOB,
∴△BOD∽△AOB,
∴$\frac{OD}{OB}$=$\frac{OB}{OA}$,
∴OD=$\frac{2×2}{4}$=1,
∴BD=$\sqrt{O{B}^{2}-O{D}^{2}}$=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∴B(1,$\sqrt{3}$).
故答案为(1,$\sqrt{3}$).
点评 本题考查了切线的性质,三角形相似的判定和性质,勾股定理的应用以及一次函数图象上点的坐标特征,作出辅助线构建直角三角形是解题的关键.

练习册系列答案
相关题目
12.已知二次函数y=x2-x+a(a>0),当自变量x取m时,其相应的函数值小于0,那么下列结论中正确的是( )
| A. | m-1>0 | B. | m-1<0 | ||
| C. | m-1=0 | D. | m-1与0的大小关系不确定 |
13.一次函数y=2x+1的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.将二次函数y=$\frac{1}{2}{x^2}$的图象向左移1个单位,再向下移2个单位后所得函数的关系式为( )
| A. | y=$\frac{1}{2}{({x+1})^2}$-2 | B. | y=$\frac{1}{2}{({x-1})^2}$-2 | C. | y=$\frac{1}{2}{({x+1})^2}$+2 | D. | y=$\frac{1}{2}{({x-1})^2}$+2 |
12.已知x2+3x+4=6,则3x2+9x-2的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 如图,在平面直角坐标系中,过格点A、B、C作一圆弧.
如图,在平面直角坐标系中,过格点A、B、C作一圆弧. 如图,数轴上点A表示的数为a,化简:|a-1|+2|a+3|=a+7.(用含a代数式表示)
如图,数轴上点A表示的数为a,化简:|a-1|+2|a+3|=a+7.(用含a代数式表示)