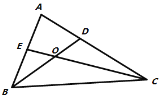
题目内容
【题目】如图,已知△![]() ,按以下步骤作图:①分别以
,按以下步骤作图:①分别以![]() 、
、![]() 为圆心,大于
为圆心,大于![]()
![]() 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点![]() 、
、![]() ;②作直线
;②作直线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,则下列结论中不一定成立的是( )
,则下列结论中不一定成立的是( )
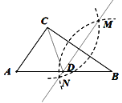
A.![]() B.△
B.△![]() 是等边三角形
是等边三角形
C.点D是AB的中点D.![]()
【答案】B
【解析】
依据直线MN是线段BC的垂直平分线,可得∠B=∠BCD不一定为30°,进而得出△ACD不是等边三角形;依据三角形内角和定理,即可得到∠ACD+∠DCB=90°,即可得到△ABC是直角三角形;依据AD=BD,即可得出D是AB的中点;依据等底同高三角形面积关系,可得![]() .
.
解:由题意可知,直线MN是线段BC的垂直平分线,可得CD=BD,∵AD=CD,
∴AD=BD,∠A=∠ACD,∠B=∠BCD,
∴∠ACD+∠BCD=90°,故A、C正确,
∵D为AB中点,可得![]() ,故D正确,
,故D正确,
∵∠B不一定为30°,
∴∠A不一定为60°,
∴B不一定成立.
故选B.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目