ΧβΡΩΡΎ»ί
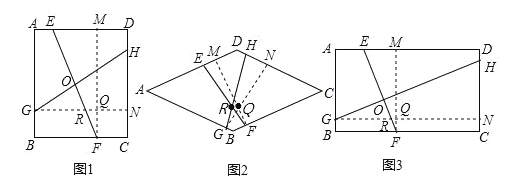
ΓΨΧβΡΩΓΩΘ®1Θ©»γΆΦ1Θ§“―÷Σ’ΐΖΫ–ΈABCDΘ§E «AD…œ“ΜΒψΘ§F «BC…œ“ΜΒψΘ§G «AB…œ“ΜΒψΘ§H «CD…œ“ΜΒψΘ§œΏΕΈEFΓΔGHΫΜ”ΎΒψOΘ§ΓœEOH=ΓœCΘ§«σ÷ΛΘΚEF=GHΘΜ
Θ®2Θ©»γΆΦ2Θ§»τΫΪΓΑ’ΐΖΫ–ΈABCDΓ±ΗΡΈΣΓΑΝβ–ΈABCDΓ±Θ§ΤδΥϊΧθΦΰ≤Μ±δΘ§ΧΫΥςœΏΕΈEF”κœΏΕΈGHΒΡΙΊœΒ≤ΔΦ”“‘÷ΛΟςΘΜ
Θ®3Θ©»γΆΦ3Θ§»τΫΪΓΑ’ΐΖΫ–ΈABCDΓ±ΗΡΈΣΓΑΨΊ–ΈABCDΓ±Θ§«“AD=mABΘ§ΤδΥϊΧθΦΰ≤Μ±δΘ§ΧΫΥςœΏΕΈEF”κœΏΕΈGHΒΡΙΊœΒ≤ΔΦ”“‘÷ΛΟςΘΜ

ΗΫΦ”ΧβΘΚΗυΨί«ΑΟφΒΡΧΫΨΩΘ§ΡψΡήΖώΫΪ±ΨΧβΆΤΙψΒΫ“ΜΑψΒΡΤΫ––ΥΡ±Ώ–Έ«ιΩωΘΩ»τΡήΘ§–¥≥ωΆΤΙψΟϋΧβΘ§Μ≠≥ωΆΦ–ΈΘ§≤Δ÷ΛΟςΘ§»τ≤ΜΡήΘ§ΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©÷ΛΟςΦϊΫβΈωΘΜΘ®2Θ©EF=GHΘΜ÷ΛΟςΦϊΫβΈωΘΜΘ®3Θ©![]() ΘΜ÷ΛΟςΦϊΫβΈωΘΜ
ΘΜ÷ΛΟςΦϊΫβΈωΘΜ
ΗΫΦ”ΧβΘΚΡήΘΜ÷ΛΟςΦϊΫβΈωΘΜ
ΓΨΫβΈωΓΩ
Θ®1Θ©ΙΐΒψFΉςFMΓΆAD”ΎMΘ§ΙΐΒψGΉςGNΓΆCD”ΎNΘ§“Ή÷ΛΓςGNHΓ’ΓςFMEΘ§ΗυΨί»ΪΒ»»ΐΫ«–ΈΒΡ–‘÷ Φ¥Ω…÷ΛΒΟΫα¬έΘΜΘ®2Θ©EF=GHΘ§ΙΐΒψFΉςFMΓΆAD”ΎMΘ§ΙΐΒψGΉςGNΓΆCD”ΎNΘ§…ηEFΓΔGNΫΜ”ΎRΓΔGNΓΔMFΫΜ”ΎQΘ§÷ΛΟςΓςGNHΓ’ΓςFMEΘ§Θ§ΗυΨί»ΪΒ»»ΐΫ«–ΈΒΡ–‘÷ Φ¥Ω…÷ΛΒΟΫα¬έΘΜΘ®3Θ©ΙΐΒψFΉςFMΓΆAD”ΎMΘ§ΙΐΒψGΉςGNΓΆCD”ΎNΘ§…ηEFΓΔGNΫΜ”ΎRΓΔGNΓΔMFΫΜ”ΎQΘ§÷ΛΟςΓςGNHΓΉΓςFMEΘ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ Φ¥Ω…÷ΛΒΟΫα¬έΘΜΗΫΦ”ΧβΘΚ»γΆΦΘ§ΙΐΒψFΉςFMΓΆAD”ΎMΘ§ΙΐΒψGΉςGNΓΆCD”ΎNΘ§…ηEFΓΔGNΫΜ”ΎRΓΔGNΓΔMFΫΜ”ΎQΘ§÷ΛΟςΓςGNHΓΉΓςFMEΘ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ ΦΑΘ®3Θ©ΒΡΫα¬έΦ¥Ω…«σΫβ.
Θ®1Θ©»γΆΦ1Θ§ΙΐΒψFΉςFMΓΆAD”ΎMΘ§ΙΐΒψGΉςGNΓΆCD”ΎNΘ§
‘ρFM=GN=AD=BCΘ§«“GNΓΆFMΘ§…ηΥϋΟ«ΒΡ¥ΙΉψΈΣQΘ§…ηEFΓΔGNΫΜ”ΎR
ΓΏΓœGOF=ΓœA=90ΓψΘ§
ΓύΓœOGR=90Γψ©¹ΓœGRO=90Γψ©¹ΓœQRF=ΓœOFMΘ°
ΓΏΓœGNH=ΓœFME=90ΓψΘ§FM=GNΘ§
ΓύΓςGNHΓ’ΓςFMEΘ°
ΓύEF=GHΘ°
Θ®2Θ©»γΆΦ2Θ§ΙΐΒψFΉςFMΓΆAD”ΎMΘ§ΙΐΒψGΉςGNΓΆCD”ΎNΘ§…ηEFΓΔGNΫΜ”ΎRΓΔGNΓΔMFΫΜ”ΎQΘ§
‘ΎΥΡ±Ώ–ΈMQND÷–Θ§ΓœQMD=ΓœQND=90Γψ
ΓύΓœADC+ΓœMQN=180ΓψΘ°
ΓύΓœMQN=ΓœA=ΓœGOFΘ°
ΓΏΓœORG=ΓœQRFΘ§
ΓύΓœHGN=ΓœEFMΘ°
ΓΏΓœA=ΓœCΘ§AB=BCΘ§
ΓύFM=ABsinA=BCsinC=GNΘ°
ΓΏΓœFEM=ΓœGNH=90ΓψΘ§
ΓύΓςGNHΓ’ΓςFMEΘ°
ΓύEF=GHΘ°
Θ®3Θ©»γΆΦ3Θ§ΙΐΒψFΉςFMΓΆAD”ΎMΘ§ΙΐΒψGΉςGNΓΆCD”ΎNΘ§…ηEFΓΔGNΫΜ”ΎRΓΔGNΓΔMFΫΜ”ΎQΘ§
ΓΏΓœGOF=ΓœA=90ΓψΘ§
ΓύΓœOGR=90Γψ©¹ΓœGRO=90Γψ©¹ΓœQRF=ΓœOFMΘ°
ΓΏΓœGNH=ΓœFME=90ΓψΘ§
ΓύΓςGNHΓΉΓςFMEΘ°
Γύ![]() Θ°
Θ°
ÿGN=ADȧFM=AB,AD=mABȧ
Γύ![]() .
.
ΗΫΦ”ΧβΘΚ
“―÷ΣΤΫ––ΥΡ±Ώ–ΈABCDΘ§E «AD…œ“ΜΒψΘ§F «BC…œ“ΜΒψΘ§G «AB…œ“ΜΒψΘ§H «CD…œ“ΜΒψΘ§œΏΕΈEFΓΔGHΫΜ”ΎΒψOΘ§ΓœEOH=ΓœCΘ§AD=mABΘ§‘ρGH=mEFΘ°
÷ΛΟςΘΚ»γΆΦΘ§ΙΐΒψFΉςFMΓΆAD”ΎMΘ§ΙΐΒψGΉςGNΓΆCD”ΎNΘ§…ηEFΓΔGNΫΜ”ΎRΓΔGNΓΔMFΫΜ”ΎQΘ§
‘ΎΥΡ±Ώ–ΈMQND÷–Θ§ΓœQMD=ΓœQND=90ΓψΘ§
ΓύΓœMDN+ΓœMQN=180ΓψΘ°
ΓύΓœMQN=ΓœA=ΓœGOFΘ°
ΓΏΓœORG=ΓœQRFΘ§
ΓύΓœHGN=ΓœEFMΘ°
ΓΏΓœFME=ΓœGNH=90ΓψΘ§
ΓύΓςGNHΓΉΓςFMEΘ°
Γύ![]() =mΘ°
=mΘ°
Φ¥GH=mEFΘ°

 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ