题目内容
【题目】阅读下面材料,完成相应任务:



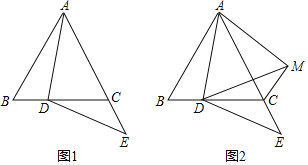
(1)小明在研究命题①时,在图1的正方形网格中画出两个符合条件的四边形.由此判断命题①是 命题(填“真”或“假”).
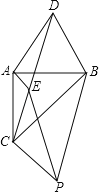
(2)小彬经过探究发现命题②是真命题.请你结合图2证明这一命题.
(3)小颖经过探究又提出了一个新的命题:“若![]() ,
,![]() ,
,![]() , , ,则四边形
, , ,则四边形![]() ≌四边形
≌四边形![]() ”请在横线上填写两个关于“角”的条件,使该命题为真命题.
”请在横线上填写两个关于“角”的条件,使该命题为真命题.
【答案】(1)假;(2)见解析;(3) ![]() ,
,![]() .
.
【解析】
(1)连接AC,延长BC到E,过点E作EF∥CD,交AD的延长线于点F,则∠E=∠BCD,∠F=∠ADC,将四边形ABEF平移得到四边形A′B′C′D′,则AB=A′B′,∠A=∠A′,∠B=∠B′,∠C=∠C′,∠D=∠D′,而BC≠B′C′,AD≠A′D′,得出四边形ABCD和四边形A′B′C′D′不全等,即可得出结论;
(2)连接BD,B′D′,证明△ABD≌△A′B′D′,得出BD=B′D′,∠ABD=∠A′B′D′,∠ADB=∠A′D′B′,再证明△BCD≌△B′C′D′,得出∠C=∠C′,∠CBD=∠C′B′D′,∠BDC=∠B′D′C′,证出∠ABC=∠A′B′C′,∠CDA=∠C′D′A′,即可得出结论;
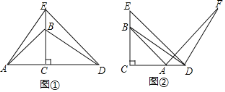
(3)连接AC、A′C′,证明△ABC≌△A′B′C′,得出AC=A′C′,∠BAC=∠B′A′C′,∠BCA=∠B′C′A′,得出∠ACD=∠A′C′D′,再证明△ACD≌△A′C′D′,得出AD=A′D′,∠D=∠D′,∠CAD=∠C′A′D′,证出∠BAD=∠B′A′D′,即可得出结论.
(1)假;
(2)连接BD、B’D’
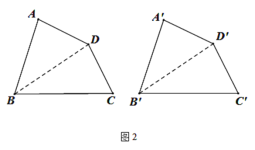
在△ABD与 △A’B’D’中

∴△ABD≌△A’B’D’(SAS)
∴BD=B’D’ ∠ABD=∠A’B’D’ ∠ADB=∠A’D’B’
在△BCD与 △B’C’D’中

∴△BCD≌△B’C’D’(SSS)
∴∠C=∠C’ ∠CBD=∠C’B’D’ ∠CDB=∠C’D’B’
∴∠ABD+∠CBD=∠A’B’D’+∠C’B’D’
∠ADB+∠CDB=∠A’D’B’+∠C’D’B’
即∠ABC=∠A’B’C’ ∠ADC=∠A’D’C’
∴四边形![]() ≌四边形
≌四边形![]()
(3)![]() ,∠C=∠C’
,∠C=∠C’

 小学能力测试卷系列答案
小学能力测试卷系列答案