Question

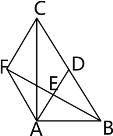
【题目】如图，AB＝AD，AC＝AE，BC＝DE，点E在BC上．

（1）求证：△ABC≌△ADE；（2）求证：∠EAC＝∠DEB．

Answer 1

【答案】（1）见解析；（2）见解析．

【解析】

（1）用“SSS”证明即可；

（2）借助全等三角形的性质及角的和差求出∠DAB＝∠EAC，再利用三角形内角和定理求出∠DEB＝∠DAB，即可说明∠EAC＝∠DEB．

解：（1）∵AB＝AD，AC＝AE，BC＝DE，

∴△ABC≌△ADE（SSS）；

（2）由△ABC≌△ADE，

则∠D＝∠B，∠DAE＝∠BAC．

∴∠DAE﹣∠ABE＝∠BAC﹣∠BAE，即∠DAB＝∠EAC．

设AB和DE交于点O，∵∠DOA＝BOE，∠D＝∠B，

∴∠DEB＝∠DAB．

∴∠EAC＝∠DEB．