题目内容
当m为何值时,使函数y=x2-4x+m-1的值恒大于0恒成立.
考点:抛物线与x轴的交点
专题:计算题
分析:由于抛物线开口向上,要使函数y=x2-4x+m-1的值恒大于0恒成立,则抛物线都在x轴上方,所以抛物线与x轴没有交点,于是得到△=(-4)2-4(m-1)<0,然后解不等式即可.
解答:解:抛物线y=x2-4x+m-1的开口向上,当抛物线与x轴没有交点时,即抛物线都在x轴上方,
所以△=(-4)2-4(m-1)<0,解得m>5,
所以当m>5时,使函数y=x2-4x+m-1的值恒大于0恒成立.
所以△=(-4)2-4(m-1)<0,解得m>5,
所以当m>5时,使函数y=x2-4x+m-1的值恒大于0恒成立.
点评:本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
下列各式计算正确的是( )
A、
| |||
B、
| |||
C、
| |||
| D、(-3)2=9 |
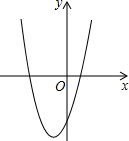 如果二次函数y=ax2+bx+c的图象如图所示,那么下列判断正确的是( )
如果二次函数y=ax2+bx+c的图象如图所示,那么下列判断正确的是( )| A、a>0,c>0 |
| B、a<0,c>0 |
| C、a>0,c<0 |
| D、a<0,c<0 |



 如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分,先从其余的小正方形中任取一个涂上阴影,则能构成这个正方体的表面展开图的共有
如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分,先从其余的小正方形中任取一个涂上阴影,则能构成这个正方体的表面展开图的共有