题目内容
阅读材料:x4-6x2+5=0是一个一元四次方程,根据该方程的特点,它的通常解法是:设x2=y,那么x4=y2,于是原方程变为y2-6y+5=0,解这个方程,得y1=1,y2=5;当y1=1时,x2=1,x=±1;当y=5时,x2=5,x=±
,所以原方程有四个根x1=1,x2=-1,x3=
,x2=-
.根据上面的方法解方程(x2-x)2-4(x2-x)-12=0.
| 5 |
| 5 |
| 5 |
考点:换元法解一元二次方程
专题:阅读型
分析:先设x2-x=t,则方程即可变形为t2-4t-12=0,解方程即可求得t即(x2-x)的值.
解答:解:设设x2-x=t,则方程即可变形为t2-4t-12=(t-6)(t+2)=0,
解得 t1=6,t2=-2.
当t=6时,x2-x=6,即(x-3)(x+2)=0,
解得 x=3或x=-2.
当t=-2时,x2-x=-2,即x2-x+2=0,
△=1-8=-7<0,
该方程无解,
所以原方程的2个根是:x1=3,x2=-2.
解得 t1=6,t2=-2.
当t=6时,x2-x=6,即(x-3)(x+2)=0,
解得 x=3或x=-2.
当t=-2时,x2-x=-2,即x2-x+2=0,
△=1-8=-7<0,
该方程无解,
所以原方程的2个根是:x1=3,x2=-2.
点评:本题主要考查换元法在解一元二次方程中的应用.换元法是借助引进辅助元素,将问题进行转化的一种解题方法.这种方法在解题过程中,把某个式子看作一个整体,用一个字母去代表它,实行等量替换.这样做,常能使问题化繁为简,化难为易,形象直观.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
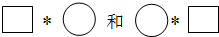 已知x、y为有理数,如果规定一种运算*,其意义是x*y=xy+1,试根据这种运算完成下列各题.
已知x、y为有理数,如果规定一种运算*,其意义是x*y=xy+1,试根据这种运算完成下列各题. 如图,某数学兴趣小组在活动课上测量学校旗杆高度,已知小红与旗杆相距12米,且小红的眼睛与地面的距离(CD)是1.5m,看旗杆顶部A的仰角为30°,求旗杆AB的高度.(参考数据:
如图,某数学兴趣小组在活动课上测量学校旗杆高度,已知小红与旗杆相距12米,且小红的眼睛与地面的距离(CD)是1.5m,看旗杆顶部A的仰角为30°,求旗杆AB的高度.(参考数据: