题目内容
已知△ADE∽△ABC，且AD=EC，DB=1cm，AE=4cm，BC=5cm，求DE的长．
考点：相似三角形的性质
专题：
分析：首先根据题意画出图形，然后由△ADE∽△ABC，根据相似三角形的对应边成比例，即可求得答案．
解答：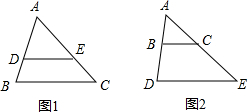
解：设AD=EC=xcm，
如图1，∵DB=1cm，AE=4cm，BC=5cm，
∴AB=x+1（cm），AC=4+x（cm），
∵△ADE∽△ABC，
∴
=
=
，
∴
=
=
，
解得：x=2，
∴DE=
；
如图2，∵DB=1cm，AE=4cm，BC=5cm，
∴AB=x-1（cm），ac=4-x（cm），
∵△ADE∽△ABC，
∴
=
=
，
∴
=
=
，
解得：x=2，
∴DE=10，
综上可得：DE=
或10．
解：设AD=EC=xcm，如图1，∵DB=1cm，AE=4cm，BC=5cm，
∴AB=x+1（cm），AC=4+x（cm），
∵△ADE∽△ABC，
∴
| AD |
| AB |
| AE |
| AC |
| DE |
| BC |
∴
| x |
| x+1 |
| 4 |
| x+4 |
| DE |
| 5 |
解得：x=2，
∴DE=
| 10 |
| 3 |
如图2，∵DB=1cm，AE=4cm，BC=5cm，
∴AB=x-1（cm），ac=4-x（cm），
∵△ADE∽△ABC，
∴
| AD |
| AB |
| AE |
| AC |
| DE |
| BC |
∴
| x |
| x-1 |
| 4 |
| 4-x |
| DE |
| 5 |
解得：x=2，
∴DE=10，
综上可得：DE=
| 10 |
| 3 |
点评：此题考查了相似三角形的性质．此题难度适中，注意掌握数形结合思想、分类讨论思想与方程思想的应用．
练习册系列答案
相关题目
如图，?ABCD的顶点A、B的坐标分别是A（1，0）、B（0，-2），顶点C、D在双曲线y=