题目内容
3. 如图,已知直线y=3-x交x轴于点A,交y轴于点B.双曲线y=$\frac{2}{x}$(x>0)与直线交于点C、点D.点P是双曲线上位于C、D两点之间的一动点,过点P作y 轴的垂线交y轴于点F,交直线与点N.过点P作x轴的垂线交x轴于点E,交直线于点M.则BM•AN的值为( )
如图,已知直线y=3-x交x轴于点A,交y轴于点B.双曲线y=$\frac{2}{x}$(x>0)与直线交于点C、点D.点P是双曲线上位于C、D两点之间的一动点,过点P作y 轴的垂线交y轴于点F,交直线与点N.过点P作x轴的垂线交x轴于点E,交直线于点M.则BM•AN的值为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 4$\sqrt{2}$ |
分析 过点M作MG⊥OB于G,过点N作NH⊥OA于H,然后由直线y=4-x交x轴、y轴于A、B两点,求得点A与B的坐标,则可得OA=OB,即可得△AOB,△BGM,△AHN是等腰直角三角形,则可得AN•BM=2GM•HN,再由矩形的性质和反比例函数的性质即可得出结论.
解答 解:过点M作MG⊥OB于G,过点N作NH⊥OA于H,如图所示: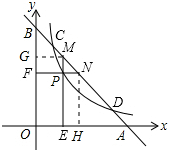
∵直线y=4-x交x轴、y轴于A、B两点,
∴A(4,0),B(0,4),
∴OA=OB,
∴∠ABO=∠BAO=45°,
∴BG=GM,AH=HN,
∵PE⊥OA,PF⊥OB,
∴四边形GMPF与EHNP是矩形,
∴GM=PF,HM=PE,
∵P是反比例函数y=$\frac{2}{x}$图象上的一点,
∴PF′PE=2,
∴GM•HN=2,
在Rt△BGM中,BM=$\frac{GM}{sin45°}$=$\sqrt{2}$GM,
在Rt△AHN中,AN=$\frac{HN}{sin45°}$=$\sqrt{2}$HN,
∴AN′BM=$\sqrt{2}$GM•$\sqrt{2}$HN=2GM•HN=4.
故选C.
点评 此题考查了反比例函数的性质,以及矩形、等腰直角三角形的性质.解题的关键是注意数形结合与转化思想的应用.

练习册系列答案
相关题目
13.某车间有26名工人,每人每天能生产螺栓12个或螺母18个,一个螺栓与两个螺母配套.要使每天生产的螺栓与螺母配套,应如何安排生产?若设有x名工人生产螺栓,则可列方程( )
| A. | 12x=18(26-x) | B. | 18x=12(26-x) | C. | 2×12x=18(26-x) | D. | 12x=2×18(26-x) |
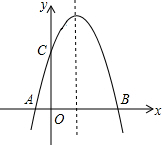 如图,已知抛物线y=ax2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,3).
如图,已知抛物线y=ax2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C(0,3).