题目内容
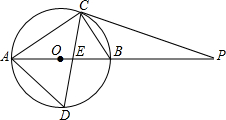 如图,⊙O的直径AB为10,弦BC为6,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE
如图,⊙O的直径AB为10,弦BC为6,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE(1)求AC、AD的长;
(2)试判断直线PC与圆⊙O的位置关系,并说明理由;
(3)直接写出CD的长为
考点:切线的判定
专题:计算题
分析:(1)连结BD,如图,根据圆周角定理由AB为直径得∠ACB=90°,则可利用勾股定理计算出AC=8;由DC平分∠ACB得∠ACD=∠BCD=45°,根据圆周角定理得∠DAB=∠DBA=45°,则△ADB为等腰直角三角形,所以AD=
AB=5
;
(2)连结OC,由PC=PE得∠PCE=∠PEC,利用三角形外角性质得∠PEC=∠A+∠ACE=∠A+45°,加上∠A=90°-∠ABC,∠ABC=∠OCB,于是可得到∠PCE=90°-∠OCB+45°=90°-(∠OCE+45°)+45°,则∠OCE+∠PCE=90°,于是根据切线的判定定理可得PC为⊙O的切线;
(3)点I为Rt△ABC的内心,连结BI,作IF⊥BC于F,如图,证明BD=BI,得到BI=DA=5
,再根据直角三角形内切圆的半径得IF=2,则CI=2
,所以CD=CI+DI=7
.
| ||
| 2 |
| 2 |
(2)连结OC,由PC=PE得∠PCE=∠PEC,利用三角形外角性质得∠PEC=∠A+∠ACE=∠A+45°,加上∠A=90°-∠ABC,∠ABC=∠OCB,于是可得到∠PCE=90°-∠OCB+45°=90°-(∠OCE+45°)+45°,则∠OCE+∠PCE=90°,于是根据切线的判定定理可得PC为⊙O的切线;
(3)点I为Rt△ABC的内心,连结BI,作IF⊥BC于F,如图,证明BD=BI,得到BI=DA=5
| 2 |
| 2 |
| 2 |
解答:解:(1)连结BD,如图,
∵AB为直径,
∴∠ACB=90°,
在Rt△ACB中,∵AB=10,BC=6,
∴AC=
=8;
∵DC平分∠ACB,
∴∠ACD=∠BCD=45°,
∴∠DAB=∠DBA=45°,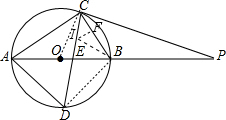
∴△ADB为等腰直角三角形,
∴AD=
AB=5
;
(2)PC与圆⊙O相切.理由如下:
连结OC,
∵PC=PE,
∴∠PCE=∠PEC,
∵∠PEC=∠A+∠ACE=∠A+45°,
而∠A=90°-∠ABC,∠ABC=∠OCB,
∴∠PCE=90°-∠OCB+45°=90°-(∠OCE+45°)+45°,
∴∠OCE+∠PCE=90°,
即∠PCO=90°,
∴OC⊥PC,
∴PC为⊙O的切线;
(3)点I为Rt△ABC的内心,连结BI,作IF⊥BC于F,如图,
∵点I为Rt△ABC的内心,
∴BI平分∠ABC,
∵∠DIB=∠ICB+∠IBC=45°+∠IBC,∠DBI=∠DBA+∠EBI=45°+∠EBI,
∴∠DIB=∠DBI,
∴BD=BI,
∴BI=DA=5
,
∵IF=
=2,
∴CI=2
,
∴CD=CI+DI=7
.
故答案为7
.
∵AB为直径,
∴∠ACB=90°,
在Rt△ACB中,∵AB=10,BC=6,
∴AC=
| AB2-BC2 |
∵DC平分∠ACB,
∴∠ACD=∠BCD=45°,
∴∠DAB=∠DBA=45°,

∴△ADB为等腰直角三角形,
∴AD=
| ||
| 2 |
| 2 |
(2)PC与圆⊙O相切.理由如下:
连结OC,
∵PC=PE,
∴∠PCE=∠PEC,
∵∠PEC=∠A+∠ACE=∠A+45°,
而∠A=90°-∠ABC,∠ABC=∠OCB,
∴∠PCE=90°-∠OCB+45°=90°-(∠OCE+45°)+45°,
∴∠OCE+∠PCE=90°,
即∠PCO=90°,
∴OC⊥PC,
∴PC为⊙O的切线;
(3)点I为Rt△ABC的内心,连结BI,作IF⊥BC于F,如图,
∵点I为Rt△ABC的内心,
∴BI平分∠ABC,
∵∠DIB=∠ICB+∠IBC=45°+∠IBC,∠DBI=∠DBA+∠EBI=45°+∠EBI,
∴∠DIB=∠DBI,
∴BD=BI,
∴BI=DA=5
| 2 |
∵IF=
| 6+8-10 |
| 2 |
∴CI=2
| 2 |
∴CD=CI+DI=7
| 2 |
故答案为7
| 2 |
点评:本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.在判定一条直线为圆的切线时,当已知条件中未明确指出直线和圆是否有公共点时,常过圆心作该直线的垂线段,证明该线段的长等于半径;当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线.

练习册系列答案
相关题目
已知
=
=
=k(a+b+c≠0),则k=( )
| c |
| a+b |
| b |
| a+c |
| a |
| b+c |
| A、0 | ||
| B、1 | ||
| C、2 | ||
D、
|
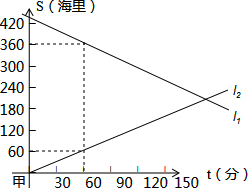 A、B两船同时从相距450海里的甲、乙两港相向而行,s(海里)表示轮船与甲港的距离,t(分钟)表示轮船行驶的时间,如图所示,l1、l2分别表示两船s与t的关系.
A、B两船同时从相距450海里的甲、乙两港相向而行,s(海里)表示轮船与甲港的距离,t(分钟)表示轮船行驶的时间,如图所示,l1、l2分别表示两船s与t的关系.