题目内容
已知:AD是△ABC的高,DE、DF是△ADB、△ADC的高,求证:B,C,E,F四点共圆.
考点:四点共圆
专题:证明题
分析:根据题意,做出图形,连接EF,根据DE、DF是△ADB、△ADC的高,证得A、E、D、F四点共圆,可得∠AEF=∠ADF,然后根据AD是△ABC的高,证明∠ADF=∠FCD,继而得出∠AEF=∠FCD,∠BEF+∠FCB=180°,然后即可证明B,C,E,F四点共圆.
解答:证明:连接EF,
∵DE⊥AB,DF⊥AC,
∴∠AED+∠AFD=180°,
即A、E、D、F四点共圆,
∴∠AEF=∠ADF,
又∵AD⊥BC,
∴∠ADF+∠CDF=90°,∠CDF+∠FCD=90°,
∴∠ADF=∠FCD,
∴∠AEF=∠FCD,
∴∠BEF+∠FCB=180°,
∴B、E、F、C四点共圆.
∵DE⊥AB,DF⊥AC,

∴∠AED+∠AFD=180°,
即A、E、D、F四点共圆,
∴∠AEF=∠ADF,
又∵AD⊥BC,
∴∠ADF+∠CDF=90°,∠CDF+∠FCD=90°,
∴∠ADF=∠FCD,
∴∠AEF=∠FCD,
∴∠BEF+∠FCB=180°,
∴B、E、F、C四点共圆.
点评:本题考查了四点共圆,解答本题的关键是根据垂直得出A、E、D、F四点共圆,然后证明∠BEF+∠FCB=180°,即可证得四点共圆.

练习册系列答案
相关题目
 如图,三角形纸片ABC,AB=10cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为( )
如图,三角形纸片ABC,AB=10cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为( )| A、9cm | B、13cm |
| C、16cm | D、10cm |
 如图是一个几何体的二视图,求该几何体的体积(л取3.14,单位:cm)
如图是一个几何体的二视图,求该几何体的体积(л取3.14,单位:cm)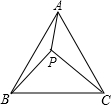 如图,已知点P是等边△ABC内一点,PA=3,PB=4,PC=5,求∠APB的度数.
如图,已知点P是等边△ABC内一点,PA=3,PB=4,PC=5,求∠APB的度数.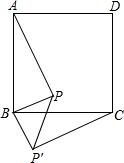 如图所示,在正方形ABCD的Rt△APB顺时针旋转至Rt△CP′B,已知正方形ABCD的面积为64cm2,AP=6cm,则PP′=
如图所示,在正方形ABCD的Rt△APB顺时针旋转至Rt△CP′B,已知正方形ABCD的面积为64cm2,AP=6cm,则PP′=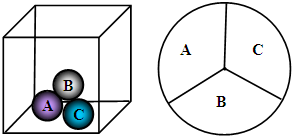
 如图:在直角坐标系中有Rt△ABC,且A(3,0),B(5,0),C(3,3);P为y轴上一点,当以P,O,B为顶点的三角形与以A,B,C为顶点的三角形相似时,求P点的坐标.
如图:在直角坐标系中有Rt△ABC,且A(3,0),B(5,0),C(3,3);P为y轴上一点,当以P,O,B为顶点的三角形与以A,B,C为顶点的三角形相似时,求P点的坐标.