题目内容
16.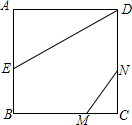 如图,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端在CB、CD上滑动,当CM为何值时,△AED与△CMN相似?
如图,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端在CB、CD上滑动,当CM为何值时,△AED与△CMN相似?
分析 根据AE=EB,△AED中AD=2AE,所以在△MNC中,分CM与AE和AD是对应边两种情况利用相似三角形对应边成比例求出CM与CN的关系,然后利用勾股定理列式计算即可.
解答 解:∵AE=EB,
∴AD=2AE,
又∵△AED与以M、N、C为顶点的三角形相似,
∴分两种情况:
①CM与AD是对应边时,CM=2CN,
∴CM2+CN2=MN2=1,
即CM2+$\frac{1}{4}$CM2=1,
解得:CM=$\frac{2\sqrt{5}}{5}$;
②CM与AE是对应边时,CM=$\frac{1}{2}$CN,
∴CM2+CN2=MN2=1,
即CM2+4CM2=1,
解得:CM=$\frac{\sqrt{5}}{5}$.
综上所述:当CM为$\frac{2\sqrt{5}}{5}$或$\frac{\sqrt{5}}{5}$时,△AED与△CMN相似.
点评 本题考查了正方形的性质、勾股定理、相似三角形的判定;主要利用相似三角形对应边成比例的性质和直角三角形勾股定理求解.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
6.二元一次方程组$\left\{\begin{array}{l}x+y=5\\ 2x-y=1\end{array}\right.$的解为$\left\{\begin{array}{l}x=2\\ y=3\end{array}\right.$,则一次函数y=5-x与y=2x-1的交点坐标为( )
| A. | (2,3) | B. | (3,2) | C. | (-2,3) | D. | (2,-3) |
7.下列计算正确的是( )
| A. | x3+x2=x5 | B. | x6÷x3=x2 | C. | x3•x2=x5 | D. | (x3)2=x5 |
4. 如图,在△ABC中,BC=8,AB的中垂线交BC于D,AC的中垂线交BC于E,则△ADE的周长等于( )
如图,在△ABC中,BC=8,AB的中垂线交BC于D,AC的中垂线交BC于E,则△ADE的周长等于( )
 如图,在△ABC中,BC=8,AB的中垂线交BC于D,AC的中垂线交BC于E,则△ADE的周长等于( )
如图,在△ABC中,BC=8,AB的中垂线交BC于D,AC的中垂线交BC于E,则△ADE的周长等于( )| A. | 8 | B. | 4 | C. | 12 | D. | 16 |
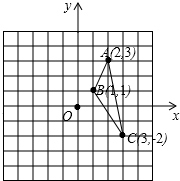 如图,利用关于坐标轴对称的点的坐标特点.
如图,利用关于坐标轴对称的点的坐标特点.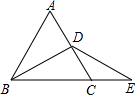 如图,D是等边△ABC的AC边上的中点,点E在BC的延长线上,DE=DB,△ABC的周长是9,则∠E=30°,CE=1.5.
如图,D是等边△ABC的AC边上的中点,点E在BC的延长线上,DE=DB,△ABC的周长是9,则∠E=30°,CE=1.5.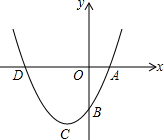 如图,已知抛物线y=x2+bx+c的图象过点A(1,0),B(0,-3).
如图,已知抛物线y=x2+bx+c的图象过点A(1,0),B(0,-3).