题目内容
5.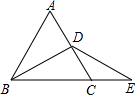 如图,D是等边△ABC的AC边上的中点,点E在BC的延长线上,DE=DB,△ABC的周长是9,则∠E=30°,CE=1.5.
如图,D是等边△ABC的AC边上的中点,点E在BC的延长线上,DE=DB,△ABC的周长是9,则∠E=30°,CE=1.5.
分析 由△ABC为等边三角形,且BD为边AC的中线,根据“三线合一”得到BD平分∠ABC,而∠ABC为60°,得到∠DBE为30°,又因为DE=DB,根据等边对等角得到∠E与∠DBE相等,故∠E也为30°;
由等边三角形的三边相等且周长为9,求出AC的长为3,且∠ACB为60°,根据∠ACB为△DCE的外角,根据三角形的外角等于与它不相邻的两个内角之和,求出∠CDE也为30°,根据等角对等边得到CD=CE,都等于边长AC的一半,从而求出CE的值.
解答 解:∵△ABC为等边三角形,D为AC边上的中点,
∴BD为∠ABC的平分线,且∠ABC=60°,
即∠DBE=30°,又DE=DB,
∴∠E=∠DBE=30°,
∵等边△ABC的周长为9,
∴AC=3,且∠ACB=60°,
∴∠CDE=∠ACB-∠E=30°,即∠CDE=∠E,
∴CD=CE=$\frac{1}{2}$AC=$\frac{3}{2}$.
故答案为:30;$\frac{3}{2}$.
点评 此题考查了等边三角形的性质,利用等边三角形的性质可以解决角与边的有关问题,尤其注意等腰三角形“三线合一”性质的运用,及“等角对等边”、“等边对等角”的运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.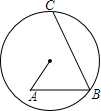 如图所示,在圆⊙O内有折线OABC,其中OA=6,BC=16,∠A=∠B=60°,则AB的长为( )
如图所示,在圆⊙O内有折线OABC,其中OA=6,BC=16,∠A=∠B=60°,则AB的长为( )
 如图所示,在圆⊙O内有折线OABC,其中OA=6,BC=16,∠A=∠B=60°,则AB的长为( )
如图所示,在圆⊙O内有折线OABC,其中OA=6,BC=16,∠A=∠B=60°,则AB的长为( )| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
10.下列计算正确的是( )
| A. | $\sqrt{8}-\sqrt{2}=\sqrt{6}$ | B. | $\frac{{\sqrt{27}-\sqrt{12}}}{3}=\sqrt{9}-\sqrt{4}$=1 | C. | $(2-\sqrt{5})(2+\sqrt{5})=1$ | D. | $\frac{{6-\sqrt{2}}}{{\sqrt{2}}}=3\sqrt{2}$-1 |

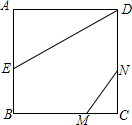 如图,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端在CB、CD上滑动,当CM为何值时,△AED与△CMN相似?
如图,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端在CB、CD上滑动,当CM为何值时,△AED与△CMN相似?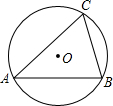 如图,△ABC是⊙O的内接三角形,∠BAC=45°,BC=4,则⊙O的直径为4$\sqrt{2}$.
如图,△ABC是⊙O的内接三角形,∠BAC=45°,BC=4,则⊙O的直径为4$\sqrt{2}$.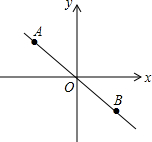 如图,A,B是正比例函数y=-$\frac{3}{4}$x图象上的两点,点A的坐标是(-4,3),点B的坐标是(4.-3),若点P是x轴上一点,且S△APB=15,求点P的坐标.
如图,A,B是正比例函数y=-$\frac{3}{4}$x图象上的两点,点A的坐标是(-4,3),点B的坐标是(4.-3),若点P是x轴上一点,且S△APB=15,求点P的坐标.