题目内容
6.二元一次方程组$\left\{\begin{array}{l}x+y=5\\ 2x-y=1\end{array}\right.$的解为$\left\{\begin{array}{l}x=2\\ y=3\end{array}\right.$,则一次函数y=5-x与y=2x-1的交点坐标为( )| A. | (2,3) | B. | (3,2) | C. | (-2,3) | D. | (2,-3) |
分析 二元一次方程可以化为一次函数,两个二元一次方程组的解就是两个函数的交点坐标.
解答 解:∵二元一次方程组$\left\{\begin{array}{l}x+y=5\\ 2x-y=1\end{array}\right.$的解为$\left\{\begin{array}{l}x=2\\ y=3\end{array}\right.$,
∴一次函数y=5-x与y=2x-1的交点坐标为(2,3),
故选A.
点评 本题主要考查了一次函数与二元一次方程组的关系,满足解析式的点就在函数的图象上,在函数的图象上的点,就一定满足函数解析式.函数图象交点坐标为两函数解析式组成的方程组的解.

练习册系列答案
相关题目
16.下列各组数中,数值相等的是( )
| A. | 34和43 | B. | -42和(-4)2 | C. | -23和(-2)3 | D. | (-2×3)2和-42×3 |
17.下列各式成立的是( )
| A. | $\sqrt{25}$=±5 | B. | $\root{3}{-27}$=3 | C. | $\root{3}{64}$=±4 | D. | $\sqrt{{{(-3)}^2}}$=3 |
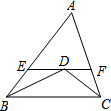 如图,在△ABC中,AB=8,BC=6,AC=5,∠B、∠C的角平分线相交于点D,过D作EF∥BC交AB于点E,交AC于点F,则△AEF的周长等于13.
如图,在△ABC中,AB=8,BC=6,AC=5,∠B、∠C的角平分线相交于点D,过D作EF∥BC交AB于点E,交AC于点F,则△AEF的周长等于13.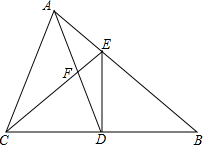 已知:如图,在△ABC中,D是BC边上的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.
已知:如图,在△ABC中,D是BC边上的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.
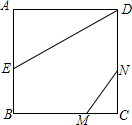 如图,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端在CB、CD上滑动,当CM为何值时,△AED与△CMN相似?
如图,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端在CB、CD上滑动,当CM为何值时,△AED与△CMN相似?