题目内容
18.某玩具厂生产一种玩具,本着控制固定成本,降价促销的原则,使生产的玩具能够全部售出.据市场调查,若按每个玩具280元销售时,每月可销售300个.若销售单价每降低1元,每月可多售出2个.据统计,每个玩具的固定成本Q(元)与月产销量y(个)满足如下关系:| 月产销量y(个) | … | 160 | 200 | 240 | 300 | … |
| 每个玩具的固定成本Q(元) | … | 60 | 48 | 40 | 32 | … |
(2)求每个玩具的固定成本Q(元)与月产销量y(个)之间的函数关系式;
(3)若每个玩具的固定成本为30元,则它占销售单价的几分之几?
(4)若该厂这种玩具的月产销量不超过400个,则每个玩具的固定成本至少为多少元?销售单价最低为多少元?
分析 (1)设y=kx+b,把(280,300),(279,302)代入解方程组即可.
(2)观察函数表可知两个变量的乘积为定值,所以固定成本Q(元)与月产销量y(个)之间存在反比例函数关系,不妨设Q=$\frac{m}{y}$,由此即可解决问题.
(3)求出销售价即可解决问题.
(4)根据条件分别列出不等式即可解决问题.
解答 解;(1)由于销售单价每降低1元,每月可多售出2个,所以月产销量y(个)与销售单价x (元)之间存在一次函数关系,不妨设y=kx+b,则(280,300),(279,302)满足函数关系式,得$\left\{\begin{array}{l}{280k+b=300}\\{279k+b=302}\end{array}\right.$解得$\left\{\begin{array}{l}{k=-2}\\{b=860}\end{array}\right.$,
产销量y(个)与销售单价x (元)之间的函数关系式为y=-2x+860.
(2)观察函数表可知两个变量的乘积为定值,所以固定成本Q(元)与月产销量y(个)之间存在反比例函数关系,不妨设Q=$\frac{m}{y}$,将Q=60,y=160代入得到m=9600,
此时Q=$\frac{9600}{y}$.
(3)当Q=30时,y=320,由(1)可知y=-2x+860,所以x=270,即销售单价为270元,
由于$\frac{30}{270}$=$\frac{1}{9}$,∴成本占销售价的$\frac{1}{9}$.
(4)若y≤400,则Q≥$\frac{9600}{400}$,即Q≥24,固定成本至少是24元,
400≥-2x+860,解得x≥230,即销售单价最低为230元.
点评 本题考查一次函数的应用、不等式,成本,销售价、销售量之间的关系,解题的关键是理解题意,灵活应用待定系数法解决问题,属于中考常考题型.

| A. | x3•x2=x5 | B. | (x-1)2=x2-1 | C. | (a3)2=a9 | D. | x(x+1)=x2+1 |
| A. | $\frac{1}{2}$x(x-1)=45 | B. | $\frac{1}{2}$x(x+1)=45 | C. | x(x-1)=45 | D. | x(x+1)=45 |
 如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )
如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{8\sqrt{13}}{13}$ | D. | $\frac{12\sqrt{13}}{13}$ |
| A. | 275×1012 | B. | 2.75×1014 | C. | 2.75×1013 | D. | 2.75×1012 |
 若将两个立方体图形按如图所示的方式放置,则所构成的几何体的左视图可能是( )
若将两个立方体图形按如图所示的方式放置,则所构成的几何体的左视图可能是( )




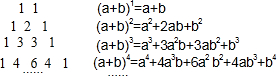 我国南宋数学家杨辉用三角形解释二项和的乘方规律,称之为“杨辉三角”.这个三角形给出了(a+b)n(n=1,2,3,4…)的展开式的系数规律(按a的次数由大到小的顺序):
我国南宋数学家杨辉用三角形解释二项和的乘方规律,称之为“杨辉三角”.这个三角形给出了(a+b)n(n=1,2,3,4…)的展开式的系数规律(按a的次数由大到小的顺序):